精英家教網(wǎng)> 2025年同步練習(xí)冊(cè)配套檢測(cè)卷九年級(jí)數(shù)學(xué)上冊(cè)魯教版五四制 > 第1頁(yè) 參考答案
2025年同步練習(xí)冊(cè)配套檢測(cè)卷九年級(jí)數(shù)學(xué)上冊(cè)魯教版五四制
注:目前有些書(shū)本章節(jié)名稱(chēng)可能整理的還不是很完善,但都是按照順序排列的,請(qǐng)同學(xué)們按照順序仔細(xì)查找。練習(xí)冊(cè)2025年同步練習(xí)冊(cè)配套檢測(cè)卷九年級(jí)數(shù)學(xué)上冊(cè)魯教版五四制答案主要是用來(lái)給同學(xué)們做完題方便對(duì)答案用的,請(qǐng)勿直接抄襲。
1. 給出下列函數(shù):①$y = 2x - 3$;②$y = \frac{1}{x}$;③$y = - 3x$。其中符合“當(dāng)$x>0$時(shí),函數(shù)值$y隨自變量的x$增大而減小”的是(
D
)
A.①③
B.③④
C.②④
D.②③
答案:D
解析:
① 對(duì)于函數(shù) $y = 2x - 3$,它是一個(gè)一次函數(shù),其斜率為 $2$,是一個(gè)正數(shù),所以當(dāng) $x > 0$ 時(shí),函數(shù)值 $y$ 隨 $x$ 的增大而增大,不符合題意。
② 對(duì)于函數(shù) $y = \frac{1}{x}$,它是一個(gè)反比例函數(shù)。
根據(jù)反比例函數(shù)的性質(zhì),當(dāng) $x > 0$ 時(shí),$y$ 隨 $x$ 的增大而減小,符合題意。
③ 對(duì)于函數(shù) $y = -3x$,它是一個(gè)一次函數(shù),其斜率為 $-3$,是一個(gè)負(fù)數(shù),所以當(dāng) $x > 0$ 時(shí),函數(shù)值 $y$ 隨 $x$ 的增大而減小,符合題意。
(題目中只給出了三個(gè)函數(shù),沒(méi)有第四個(gè)函數(shù),所以④不用考慮)
綜合以上分析,符合題意的有②和③。
2. 若點(diǎn)$A(x_{1}, - 6)$,$B(x_{2}, - 2)$,$C(x_{3},2)在反比例函數(shù)y = - \frac{4}{x}$的圖象上,則$x_{1}$,$x_{2}$,$x_{3}$的大小關(guān)系是(
B
)
A.$x_{1}<x_{2}<x_{3}$
B.$x_{3}<x_{1}<x_{2}$
C.$x_{2}<x_{3}<x_{1}$
D.$x_{2}<x_{1}<x_{3}$
答案:B
解析:
因?yàn)辄c(diǎn)$A(x_{1}, - 6)$,$B(x_{2}, - 2)$,$C(x_{3},2)$在反比例函數(shù)$y = -\frac{4}{x}$的圖象上,將各點(diǎn)的$y$坐標(biāo)代入方程:
對(duì)于點(diǎn)$A$,$ -6 = -\frac{4}{x_{1}} \implies x_{1} = \frac{4}{6} = \frac{2}{3}$。
對(duì)于點(diǎn)$B$,$ -2 = -\frac{4}{x_{2}} \implies x_{2} = \frac{4}{2} = 2$。
對(duì)于點(diǎn)$C$,$2 = -\frac{4}{x_{3}} \implies x_{3} = -\frac{4}{2} = -2$。
比較$x_{1}$,$x_{2}$,$x_{3}$的大小,得到$x_{3} < x_{1} < x_{2}$。
3. 在同一坐標(biāo)系中,函數(shù)$y = \frac{k}{x}和y = - kx + 3$的大致圖象可能是(
D
)
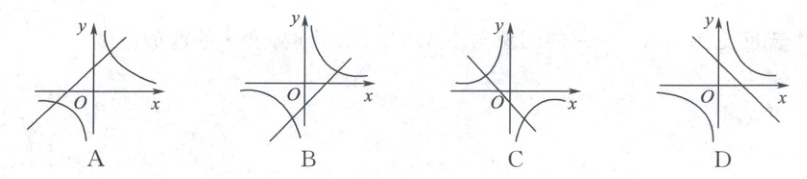
答案:D
解析:
1. 一次函數(shù)$y = -kx + 3$與y軸交于點(diǎn)$(0, 3)$,故直線必過(guò)y軸正半軸,排除B、C;
2. 若直線$y = -kx + 3$為增函數(shù)(從左到右上升),則斜率$-k > 0$,即$k < 0$,此時(shí)反比例函數(shù)$y = \frac{k}{x}$圖象在第二、四象限,A中雙曲線在第一、三象限,矛盾,排除A;
3. 若直線為減函數(shù)(從左到右下降),則斜率$-k < 0$,即$k > 0$,此時(shí)反比例函數(shù)$y = \frac{k}{x}$圖象在第一、三象限,D符合.
4. 點(diǎn)$M(x_{1},y_{1})和點(diǎn)N(x_{2},y_{2})在反比例函數(shù)y = \frac{k^{2} - 2k + 3}{x}$($k$為常數(shù))的圖象上。若$x_{1}<0<x_{2}$,則$y_{1}$,$y_{2}$,$0$的大小關(guān)系為(
C
)
A.$y_{1}<y_{2}<0$
B.$y_{1}>y_{2}>0$
C.$y_{1}<0<y_{2}$
D.$y_{1}>0>y_{2}$
答案:C
解析:
先化簡(jiǎn)反比例函數(shù)的比例系數(shù):$k^2 - 2k + 3 = (k - 1)^2 + 2$,因?yàn)?(k - 1)^2 \geq 0$,所以$(k - 1)^2 + 2 \geq 2 > 0$,即比例系數(shù)為正數(shù)。反比例函數(shù)$y = \frac{m}{x}$($m > 0$)的圖象在第一、三象限,在每個(gè)象限內(nèi)$y$隨$x$的增大而減小。已知$x_1 < 0 < x_2$,則點(diǎn)$M$在第三象限,$y_1 < 0$;點(diǎn)$N$在第一象限,$y_2 > 0$,所以$y_1 < 0 < y_2$。
5. 如果矩形的面積為 8,那么它的長(zhǎng)$y與寬x$的函數(shù)關(guān)系圖象大致表示為(
B
)
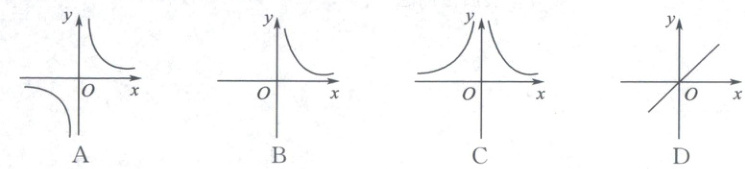
答案:B
解析:
由矩形的面積公式$S=xy$,已知面積為8,可得$xy=8$,變形得到$y=\frac{8}{x}$。
因?yàn)?x\gt0$,$y\gt0$,所以函數(shù)圖象只在第一象限。
該函數(shù)是反比例函數(shù),其圖象是雙曲線。


