Question

【題目】如圖，平行四邊形ABCD中，BC=2AB=4，∠ABC=60°，PA⊥AD，E，F分別為BC，PE的中點，AF⊥平面PED．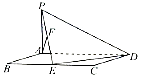
（1）求證：PA⊥平面ABCD；
（2）求直線BF與平面AFD所成角的正弦值．

Answer 1

【答案】
（1）解：連接AE，

∵AF⊥平面PED，ED平面PED，

∴AF⊥ED，

在平行四邊形ABCD中，BC=2AB=4，∠ABC=60°，

∴AE=2， ，

∴AE2+ED2=AD2，∴AE⊥ED，

又∵AF∩AE=A，AF平面PAE，PA平面PAE，

∴ED⊥平面PAE，∵PA平面PAE，

∴ED⊥PA，

又PA⊥AD，AD∩ED=D，AE平面ABCD，AD平面ABCD，

∴PA⊥平面ABCD

（2）解：以E為坐標原點，以EA，ED為x軸，y軸建立如圖所示的空間直角坐標系，

則A（0，2，0）， ， ，

∵AF⊥平面PED，所以AF⊥PE，

又F為PE中點，∴PA=AE=2，

∴P（0，2，2），F（0，1，1），

∴ ， ， ，

設平面AFD的法向量為 ，

由 ， 得， ，

令x=1，得 ．

設直線BF與平面AFD所成的角為θ，則： ，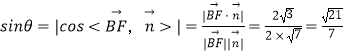

即直線BF與平面AFD所成角的正弦值為 ．

【解析】（1）利用勾股定理的逆定理得出AE⊥DE，由AF⊥平面PED得DE⊥AF，故而DE⊥平面PAE，于是DE⊥PA，結合PA⊥AD得出PA⊥平面ABCD；（2）以E為原點建立空間坐標系，求出平面ADF的法向量 ，則|cos＜ ＞|為直線BF與平面AFD所成角的正弦值．