
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上運動(
上運動(![]() 不與
不與![]() 、
、![]() 重合),連接
重合),連接![]() ,作
,作![]() ,
,![]() 交線段
交線段![]() 于
于![]() .
.
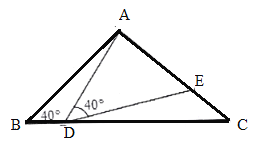
(1)當![]() 時,
時,![]() ______________
______________![]() ;點
;點![]() 從
從![]() 向
向![]() 運動時,
運動時,![]() 逐漸變____________(填“大”或“小”);
逐漸變____________(填“大”或“小”);
(2)當![]() 時,求證:
時,求證:![]() ,請說明理由;
,請說明理由;
(3)在點![]() 的運動過程中,
的運動過程中,![]() 的形狀也在改變,判斷當
的形狀也在改變,判斷當![]() 等于多少度時,
等于多少度時,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)25°;小;(2)見解析;(3)當∠BDA的度數為80°或110°時,△ADE是等腰三角形.
【解析】
(1)利用三角形內角和定理,即可求出![]() ;然后根據∠BAD的變化情況,即可判斷
;然后根據∠BAD的變化情況,即可判斷![]() 的變化情況;
的變化情況;
(2)利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AAS即可得出△ABD≌△DCE;
(3)根據等腰三角形的腰的情況分類討論,再利用等腰三角形的性質和三角形的外角即可分別求出∠BDA.
解:∵在△BAD中,∠B=40°,∠BDA=115°,
∴∠BAD=180°﹣∠B﹣∠BDA=25°;
∠BAD+∠BDA=180°﹣∠B=140°
由圖可知:點![]() 從
從![]() 向
向![]() 運動時,∠BAD逐漸變大,則
運動時,∠BAD逐漸變大,則![]() 逐漸變小.
逐漸變小.
故答案為:25°;小;
(2)∵∠B=∠C=40°,
∴∠DEC+∠EDC=180°﹣∠C=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=180°﹣∠ADE =140°,
∴∠ADB=∠DEC,
∵![]() ,
,![]()
∴![]()
在△ABD和△DCE中,

∴△ABD≌△DCE(AAS).
(3)當△ADE是等腰三角形時,∠BDA的度數為80°或110°,
①當ED=EA時,
∴∠DAE=∠EDA=40°,
∴∠BDA=∠C+DAE=80°;
②當DA=DE時,
∴∠DAE=∠DEA=![]() (180°﹣∠ADE)=70°,
(180°﹣∠ADE)=70°,
∴∠BDA=∠C+DAE=110°,
③當AD=AE時,
∠ADE=∠AED=40°
∵∠C=40°
∠AED是△EDC的外角
∴∠AED>∠C,與∠AED=40°矛盾
所以此時不成立;
綜上所述:當∠BDA的度數為80°或110°時,△ADE是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的兩條角平分線,且
的兩條角平分線,且![]() ,
,![]() 交于點
交于點![]() .
.
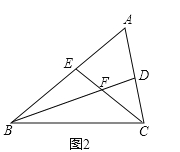
(1)如圖1,用等式表示![]() ,
,![]() ,
,![]() 這三條線段之間的數量關系,并證明你的結論;
這三條線段之間的數量關系,并證明你的結論;

小東通過觀察、實驗,提出猜想:![]() .他發現先在
.他發現先在![]() 上截取
上截取![]() ,使
,使![]() ,連接
,連接![]() ,再利用三角形全等的判定和性質證明
,再利用三角形全等的判定和性質證明![]() 即可.
即可.
①下面是小東證明該猜想的部分思路,請補充完整:
ⅰ)在![]() 上截取
上截取![]() ,使
,使![]() ,連接
,連接![]() ,則可以證明
,則可以證明![]() 與 全等,判定它們全等的依據是 ;
與 全等,判定它們全等的依據是 ;
ⅱ)由![]() ,
,![]() ,
,![]() 是
是![]() 的兩條角平分線,可以得出
的兩條角平分線,可以得出![]() °;
°;
②請直接利用ⅰ),ⅱ)已得到的結論,完成證明猜想![]() 的過程.
的過程.
(2)如圖2,若![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
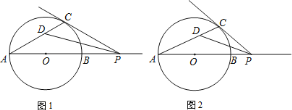
【題目】已知:![]() 為
為![]() 的直徑,
的直徑,![]() 為
為![]() 延長線上的任意一點,過點
延長線上的任意一點,過點![]() 作
作![]() 的切線,切點為
的切線,切點為![]() ,
,![]() 的平分線
的平分線![]() 與
與![]() 交于點
交于點![]() .
.
(1)如圖![]() ,若
,若![]() 恰好等于
恰好等于![]() ,求
,求![]() 的度數;
的度數;
(2)如圖![]() ,若點
,若點![]() 位于
位于![]() 中不同的位置,
中不同的位置,![]() 的結論是否仍然成立?說明你的理由.
的結論是否仍然成立?說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象經過點A(3,0),B(2,﹣3),并且以x=1為對稱軸.
(1)求此函數的解析式;
(2)作出二次函數的大致圖象;
(3)在對稱軸x=1上是否存在一點P,使△PAB中PA=PB?若存在,求出P點的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
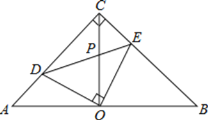
【題目】如圖,在等腰直角![]() 中,
中,![]() ,
,![]() 是斜邊
是斜邊![]() 的中點,點
的中點,點![]() 、
、![]() 分別在直角邊
分別在直角邊![]() 、
、![]() 上,且
上,且![]() ,
,![]() 交
交![]() 于點
于點![]() .則下列結論:①圖形中全等的三角形只有兩對;②
.則下列結論:①圖形中全等的三角形只有兩對;②![]() 的面積等于四邊形
的面積等于四邊形![]() 面積的2倍;③
面積的2倍;③![]() ;④
;④![]() .其中正確的結論有_______________________________(填序號)
.其中正確的結論有_______________________________(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
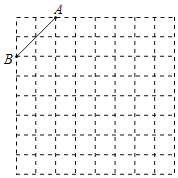
【題目】如圖是8×8的正方形網格,請在所給網格中按下列要求操作:
(1)在網格中建立平面直角坐標系,使點A的坐標為(﹣2,4),點B的坐標為(﹣4,2);
(2)在第二象限內的格點上畫一點C,連接AC,BC,使△BC成為以AB為底的等腰三角形,且腰長是無理數.
①此時點C的坐標為 ,△ABC的周長為 (結果保留根號);
②畫出△ABC關于y軸對稱的△A′B'C′(點A,B,C的對應點分別A',B',C′),并寫出A′,B′,C′的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com