
【題目】如圖,在平面直角坐標(biāo)系中,頂點(diǎn)為(2,﹣1)的拋物線交y軸于A點(diǎn),交x軸于B、C兩點(diǎn)(點(diǎn)B在點(diǎn)C的左側(cè)),已知A點(diǎn)坐標(biāo)為(0,3),連接AB.
(1)求此拋物線的解析式;
(2)過點(diǎn)B作線段AB的垂線交拋物線于點(diǎn)D,如果以點(diǎn)C為圓心的圓與直線BD相切,請判斷拋物線的對稱軸l與⊙C有怎樣的位置關(guān)系,并給出證明;
(3)已知點(diǎn)P是拋物線上的一個動點(diǎn),且位于A,C兩點(diǎn)之間,問:當(dāng)點(diǎn)P運(yùn)動到什么位置時(shí),△PAC的面積最大?并求出此時(shí)P點(diǎn)的坐標(biāo)和△PAC的最大面積.
【答案】
(1)解:設(shè)拋物線的解析式為y=a(x﹣2)2﹣1
把A(0,3)代入得:3=4a﹣1
解得:a=1,
故 y=(x﹣2)2﹣1
=x2﹣4x+3
(2)解:拋物線的對稱軸與⊙C相離
理由如下:
如圖1,過點(diǎn)C作CE⊥BD于E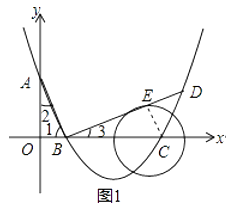
令y=0,則x2﹣4x+3=0
解得:x1=1,x2=3
則B(1,0),C(3,0),A(0,3),
故AB= ![]() ,
,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∴△AOB~△BEC
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CE= ![]()
![]() ,
,
∴BF=CE=1> ![]()
![]() ,
,
∴拋物線的對稱軸與⊙C相離
(3)解:設(shè)P(m,m2﹣4m+3),如圖2,過點(diǎn)P作作PQ∥y軸交AC于點(diǎn)Q,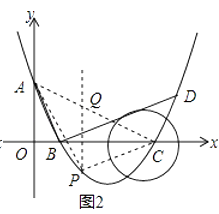
設(shè)AC的解析式為:y=kx+b,
故 ![]() ,
,
解得: ![]() ,
,
故AC的解析式為:y=﹣x+3,
則Q(m,﹣m+3),
則PQ=﹣m+3﹣(m2﹣4m+3)=﹣m2+3m,
S△PAC=S△AQP+S△CQP
= ![]() ×3(﹣m2+3m),
×3(﹣m2+3m),
=﹣ ![]() m2+
m2+ ![]() m,
m,
則m=﹣ ![]() =
= ![]() ÷3=
÷3= ![]() ,
,
把m= ![]() 代入得:﹣
代入得:﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ,
,
故p( ![]() ,﹣
,﹣ ![]() ),
),
則S△PAC的最大值= ![]() .
.
【解析】(1)可設(shè)拋物線為頂點(diǎn)式,再把(0,3)代入即可;(2)判定直線和圓的位置關(guān)系需比較“d與r的大小”,通過相似,即△AOB~△BEC,求出圓的半徑CE,圓心到直線的距離CF=d=1;(3)最值問題可利用函數(shù)思想,構(gòu)建以P的橫坐標(biāo)x為自變量、S△PAC為因變量的函數(shù),配方法求出最值.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】4月21日是重慶一中校慶日,學(xué)校每一年都要舉行校慶活動和教職工運(yùn)動會,全校分校區(qū)或年級組隊(duì)進(jìn)行角逐,今年某校區(qū)給參賽老師購買了![]() 、
、![]() 、
、![]() 三種運(yùn)動服,每一套價(jià)格分別是400元,500元,600元,其中
三種運(yùn)動服,每一套價(jià)格分別是400元,500元,600元,其中![]() 種運(yùn)動服套數(shù)是
種運(yùn)動服套數(shù)是![]() 種運(yùn)動服套數(shù)的3倍,
種運(yùn)動服套數(shù)的3倍,![]() 種運(yùn)動服套數(shù)比C種運(yùn)動服套數(shù)的2倍還多,要求購買服裝的總套數(shù)盡量多且總費(fèi)用不超過52300元,則能購買到運(yùn)動服最多_________套.
種運(yùn)動服套數(shù)比C種運(yùn)動服套數(shù)的2倍還多,要求購買服裝的總套數(shù)盡量多且總費(fèi)用不超過52300元,則能購買到運(yùn)動服最多_________套.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】從-2,-1,0,1,2,3,5這七個數(shù)中,隨機(jī)抽取一個數(shù)記為m,若數(shù)m使關(guān)于x的不等式組![]() 無解,且使關(guān)于x的一元一次方程(m-2)x=3有整數(shù)解,那么這六個數(shù)所有滿足條件的m的個數(shù)有( )
無解,且使關(guān)于x的一元一次方程(m-2)x=3有整數(shù)解,那么這六個數(shù)所有滿足條件的m的個數(shù)有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,⊙O的直徑為10,在⊙O上位于直徑AB的異側(cè)有定點(diǎn)C和動點(diǎn)P,已知BC:CA=4:3,點(diǎn)P在半圓弧AB上運(yùn)動(不與A、B兩點(diǎn)重合),過點(diǎn)C作CP的垂線CD交PB的延長線于D點(diǎn).
(1)求證:ACCD=PCBC;
(2)當(dāng)點(diǎn)P運(yùn)動到AB弧中點(diǎn)時(shí),求CD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,如圖,![]() 、
、![]() 是直線,
是直線,![]() ,
,![]() ,
,![]() .
.![]() 與
與![]() 平行嗎?為什么?
平行嗎?為什么?

解:![]() ,理由如下:
,理由如下:
∵![]() (已知)
(已知)
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() _________( )
_________( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴![]() _________(等量代換)
_________(等量代換)
∴![]() ( )
( )
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)M是AB的中點(diǎn),點(diǎn)P在MB上.分別以AP,PB為邊,作正方形APCD和正方形PBEF,連結(jié)MD和ME.設(shè)AP=a,BP=b,且a+b=10,ab=20.則圖中陰影部分的面積為________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,方格紙中每個小方格都是長為1個單位的正方形,若學(xué)校位置坐標(biāo)為A(1,2),解答以下問題:
(1)請?jiān)趫D中建立適當(dāng)?shù)闹苯亲鴺?biāo)系,并寫出圖書館B位置的坐標(biāo);

(2)若體育館位置坐標(biāo)為C(-3,3),請?jiān)谧鴺?biāo)系中標(biāo)出體育館的位置,并順次連接學(xué)校、圖書館、體育館,得到△ABC,求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一家商店進(jìn)行裝修,若請甲、乙兩個裝修組同時(shí)施工,8天可以完成,需付兩組費(fèi)用共3520元,若先請甲組單獨(dú)做6天,再請乙組單獨(dú)做12天可以完成,需付費(fèi)用3480元,問:
(1)甲,乙兩組工作一天,商店各應(yīng)付多少錢?
(2)已知甲單獨(dú)完成需12天,乙單獨(dú)完成需24天,單獨(dú)請哪個組,商店所需費(fèi)用最少?
(3)若裝修完后,商店每天可贏利200元,你認(rèn)為如何安排施工更有利于商店?請你幫助商店決策.(可用(1)(2)問的條件及結(jié)論)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com