
【題目】如圖,AD為△ABC的中線,BE為△ABD的中線.

(1)∠ABE=15°, ∠BAD=40°,求∠BED的度數;
(2)若△ABC的面積為80,BD=16,求E到BC邊的距離為多少.
【答案】(1) ∠BED的度數為55°; (2)E到BC邊的距離為2.5.
【解析】
(1)根據三角形內角與外角的性質解答即可;
(2)過E作BC邊的垂線即可得:E到BC邊的距離為EF的長,然后過A作BC邊的垂線AG,再根據三角形中位線定理求解即可.
(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)過E作BC邊的垂線,F為垂足,則EF為所求的E到BC邊的距離,過A作BC邊的垂線AG,垂足為點G,
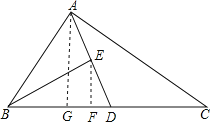
∴AD為△ABC的中線,BD=16,
∴BC=2BD=2×16=32,
∵△ABC的面積為80,
∴![]() BCAG=80,即
BCAG=80,即![]() ×32AG=80,解得AG=5,
×32AG=80,解得AG=5,
∵EF⊥BC于F,
∴EF∥AG,
∵E為AD的中點,
∴EF是△AGD的中位線,
∴EF=![]() AG=
AG=![]() ×5=2.5.
×5=2.5.
∴E到BC邊的距離為2.5.


科目:初中數學 來源: 題型:
【題目】一家商店進行裝修,若請甲、乙兩個裝修組同時施工,8天可以完成,需付兩組費用共3520元,若先請甲組單獨做6天,再請乙組單獨做12天可以完成,需付費用3480元,問:
(1)甲,乙兩組工作一天,商店各應付多少錢?
(2)已知甲單獨完成需12天,乙單獨完成需24天,單獨請哪個組,商店所需費用最少?
(3)若裝修完后,商店每天可贏利200元,你認為如何安排施工更有利于商店?請你幫助商店決策.(可用(1)(2)問的條件及結論)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某年級共有400名學生,為了解該年級學生上學的交通方式,從中隨機抽取100名學生進行問卷調查,并對調查數據進行整理、描述和分析,下面給出了部分信息
A.不同交通方式學生人數分布統計圖如下:

B.采用公共交通方式單程所花費時間(分鐘)的頻數分布直方圖如下(數據分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);

根據以上信息,完成下列問題:
(1)補全頻數分布直方圖;
(2)根據不同交通方式學生人數所占的百分比,算出“私家車方式”對應扇形的圓心角是度_____.
(3)請你估計全年級乘坐公共交通上學有_____人,其中單程不少于60分鐘的有_____人.
查看答案和解析>>
科目:初中數學 來源: 題型:
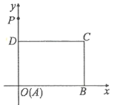
【題目】如圖,矩形ABCD在平面直角坐標系的位置如圖,A(0,0),B(6,0),D(0,4)
(1) 根據圖形直接寫出點C的坐標;
(2) 已知直線m經過點P(0,6)且把矩形ABCD分成面積相等的兩部分,請只用直尺準確地畫出直線m,并求該直線m的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,點E、F分別在邊BC、CD上,且∠EAF=∠CFF=45°
(1) 將△ADF繞點A順時針旋轉90 °,得到△ABG(如圖1),求證:BE+DF=EF;
(2) 若直線EF與AB、AD的延長線分別交于點M、N(如圖2),求證:![]()
(3) 將正方形改為長與寬不相等的矩形,其余條件不變(如圖3),直接寫出線段EF、BE、DF之間的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,線段AB=9,射線BG⊥AB,P為射線BG上一點,以AP為邊作正方形APCD,且C、D與點B在AP兩側,在線段DP取一點E,使∠EAP=∠BAP,直線CE與線段AB相交于點F(點F與點A、B不重合).

(1)求證:△AEP≌△CEP;
(2)判斷CF與AB的位置關系,并說明理由;
(3)求△AEF的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了更好地保護環境,某區污水處理廠決定購買A,B兩種型號污水處理設備10臺,其中每臺的價格、月處理污水量如下表.已知購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.

(1)求a,b的值;
(2)某區污水處理廠決定購買污水處理設備的資金既不少于108萬元也不超過110萬元,問有幾種購買方案?每月最多能處理污水多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1,是一個長為![]() ,寬為
,寬為![]() 的長方形,沿圖中虛線用剪刀平均分成四塊小長方形,然后按圖2的形狀拼成一個正方形.
的長方形,沿圖中虛線用剪刀平均分成四塊小長方形,然后按圖2的形狀拼成一個正方形.



(1)圖2中的陰影部分的面積為 ;
(2)觀察圖2,三個代數式![]() ,
,![]() ,
,![]() 之間的等量關系是 ;
之間的等量關系是 ;
(3)若![]() ,
,![]() ,求
,求![]() ;
;
(4)觀察圖3,你能得到怎樣的代數恒等式呢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com