
【題目】一只不透明的袋子中裝有4個質地、大小均相同的小球,這些小球分別標有數字3,4,5,x.甲、乙兩人每次同時從袋中各隨機摸出1個球,并計算摸出的這2個小球上數字之和,記錄后都將小球放回袋中攪勻,進行重復試驗.實驗數據如下表:
摸球總次數 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和為8”出現的頻數 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和為8”出現的頻率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列問題:
(1)如果實驗繼續進行下去,根據上表數據,出現“和為8”的頻率將穩定在它的概率附近.估計出現“和為8”的概率是;
(2)當x=7時,請用列表法或樹狀圖法計算“和為8”的概率;并判斷x=7是否可能.
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AB的垂直平分線交AB于點N,交BC的延長線于點M.
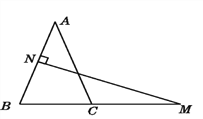
(1)若∠A=40°,求∠NMB的度數.
(2)如果將(1)中∠A的度數改為70°,其余條件不變,求∠NMB的度數.
(3)由(1)(2)你發現了什么規律?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的頂點A,B與正方形EFGH的頂點G,H同在一段拋物線上,且拋物線的頂點同時落在CD和y軸上,正方形邊AB與EF同時落在x軸上,若正方形ABCD的邊長為4,則正方形EFGH的邊長為 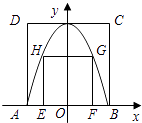
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點M,與BD相交于點N,連接BM,DN.

(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長
查看答案和解析>>
科目:初中數學 來源: 題型:
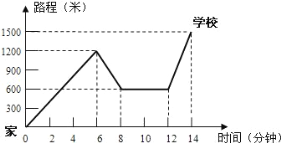
【題目】小明騎單車上學,當他騎了一段路時,想起要買某本書,于是又折回到剛經過的某書店,買到書后繼續去學校.以下是他本次上學所用的時間與路程的關系示意圖.
根據圖中提供的信息回答下列問題:
(1)小明家到學校的路程是多少米?
(2)在整個上學的途中哪個時間段小明騎車速度最快,最快的速度是多少米/分?
(3)小明在書店停留了多少分鐘?
(4)本次上學途中,小明一共行駛了多少米?一共用了多少分鐘?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,正方形ABCD與正方形AEFG的邊AB,AE(AB<AE)在一條直線上,正方形AEFG以點A為旋轉中心逆時針旋轉,設旋轉角為α.在旋轉過程中,兩個正方形只有點A重合,其它頂點均不重合,連接BE,DG.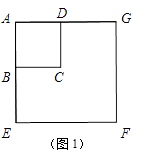
(1)當正方形AEFG旋轉至如圖2所示的位置時,求證:BE=DG;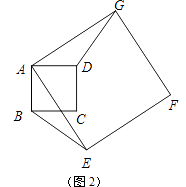
(2)如圖3,如果α=45°,AB=2,AE=3 ![]() .
.
①求BE的長;②求點A到BE的距離;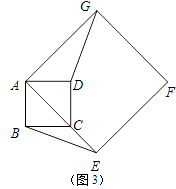
(3)當點C落在直線BE上時,連接FC,直接寫出∠FCD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分線EF分別交AD、BC于點E、F,垂足為O. 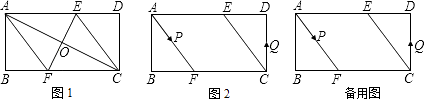
(1)如圖1,連接AF、CE.求證四邊形AFCE為菱形,并求AF的長;
(2)如圖2,動點P、Q分別從A、C兩點同時出發,沿△AFB和△CDE各邊勻速運動一周.即點P自A→F→B→A停止,點Q自C→D→E→C停止.在運動過程中, ①已知點P的速度為每秒5cm,點Q的速度為每秒4cm,運動時間為t秒,當A、C、P、Q四點為頂點的四邊形是平行四邊形時,求t的值.
②若點P、Q的運動路程分別為a、b(單位:cm,ab≠0),已知A、C、P、Q四點為頂點的四邊形是平行四邊形,求a與b滿足的數量關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖A在數軸上所對應的數為﹣2.
(1)點B在點A右邊距A點4個單位長度,求點B所對應的數;
(2)在(1)的條件下,點A以每秒2個單位長度沿數軸向左運動,點 B 以每秒2個單位長度沿數軸向右運動,當點A運動到﹣6所在的點處時,求A,B兩點間距離.
(3)在(2)的條件下,現A點靜止不動,B點再以每秒2個單位長度沿數軸向左運動時,經過多長時間A,B兩點相距4個單位長度.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com