
【題目】綜合與實踐
問題情境
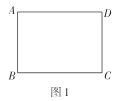
綜合與實踐課上,老師讓同學們以“折紙”為主題開展數學活動.如圖1,有一張長為4,寬為3的矩形紙片![]() (
(![]() ).
).
操作發現
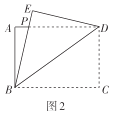
(1)快樂小組先將圖1中的矩形紙片![]() 沿直線
沿直線![]() 折疊,使得點
折疊,使得點![]() 落在點
落在點![]() 處,得到圖2,他們發現
處,得到圖2,他們發現![]() ,請你證明這個結論;
,請你證明這個結論;
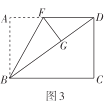
(2)創新小組將圖2中的矩形紙片展開后繼續折疊,使得點![]() 落在對角線
落在對角線![]() 上的點
上的點![]() 處,折痕為
處,折痕為![]() ,得到圖3,則折痕
,得到圖3,則折痕![]() __________;
__________;
實踐探究
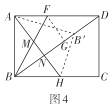
(3)前進小組在創新小組的操作基礎上,將圖3中的紙片展開,再將矩形紙片![]() 沿直線
沿直線![]() 折疊,使得點
折疊,使得點![]() 落在對角線
落在對角線![]() 上的點
上的點![]() 處,然后將紙片展平.如圖4所示,折痕
處,然后將紙片展平.如圖4所示,折痕![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,試判斷
,試判斷![]() 的形狀并證明你的結論.
的形狀并證明你的結論.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() 為等腰三角形,理由見解析.
為等腰三角形,理由見解析.
【解析】
(1)利用矩形和折疊的性質分別得到![]() ,
,![]() ,
,![]() ,
,![]() ,然后根據AAS定理證明
,然后根據AAS定理證明![]() ,從而求證
,從而求證![]() ;
;
(2)根據勾股定理求得BD的長,設AF=FG=x,然后利用折疊的性質及勾股定理列方程求出AF的值,最后再利用勾股定理求BF;
(3)利用折疊的性質得到![]() 垂直平分
垂直平分![]() ,從而得到
,從而得到![]() 及
及![]() ,然后利用等角對等邊判定三角形的形狀.
,然后利用等角對等邊判定三角形的形狀.
解:(1)如圖2,![]() 四邊形
四邊形![]() 為矩形,
為矩形,
![]() ,
,![]() ,
,
由折疊得![]() ,
,![]() ,
,
![]() ,
,![]()
![]() 在
在![]() 和
和![]() 中,
中,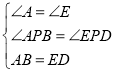
![]() ,
,
![]() ;
;
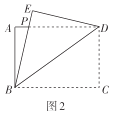
(2)如圖3,由題意可知:AB=BG=3,AD=4,∠A=∠FGB=90°
∴BD=![]()
∴DG=BD-BG=5-3=2
設AF=FG=x,則DF=4-x
在Rt△FGD中,![]()
解得:![]()
在Rt△ABF中,![]()
故答案為:![]() ;
;
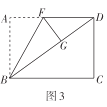
(3)如圖4,![]() 為等腰三角形.
為等腰三角形.
理由如下:
![]() 折疊得到
折疊得到![]() ,
,
![]() 垂直平分
垂直平分![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() .
.
又![]() 折疊得到
折疊得到![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 為等腰三角形.
為等腰三角形.


科目:初中數學 來源: 題型:
【題目】如圖所示,長方形紙片ABCD的長AD=9cm,寬AB=3cm,將其折疊,使點D與點B重合.
求:(1)折疊后DE的長;(2)以折痕EF為邊的正方形面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小亮利用三張卡片做游戲,卡片上分別寫有A,B,B.這些卡片除字母外完全相同,從中隨機摸出一張,記下字母后放回,充分洗勻后,再從中摸出一張,如果兩次摸到卡片字母相同則小明勝,否則小亮勝,這個游戲對雙方公平嗎?請說明現由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 邊上的高,連接
邊上的高,連接![]() ,過點
,過點![]() 作
作![]() 與點
與點![]() ,
,![]() 為
為![]() 中點,連接
中點,連接![]() ,
,![]() .
.
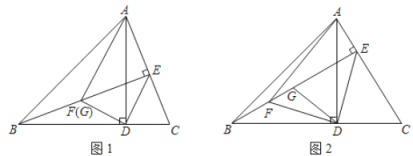
(1)如圖![]() ,若點
,若點![]() 與點
與點![]() 重合,求證:
重合,求證:![]() ;
;
(2)如圖![]() ,請寫出
,請寫出![]() 與
與![]() 之間的關系并證明.
之間的關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 是等邊三角形,D 為 CB 延長線上一點,E 為 BC 延長線上點.
(1)當 BD、BC 和 CE 滿足什么條件時,△ADB∽△EAC?
(2)當△ADB∽△EAC 時,求∠DAE 的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中Rt△AOB≌Rt△DCA,其中B(0,4),C(2,0).連接BD.

(1)求直線BD的解析式;
(2)點E是直線AD上一點,連接BE,以BE,ED為一組鄰邊作BEDF,當BEDF的面積為3時,求點E的坐標;
(3)如圖2,將△DAC沿x軸向左平移,平移距離大于0,記平移后的△DAC為△D′A′C′,連接D′A,D′B,當△D′AB為等腰三角形時,直接寫出點D′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
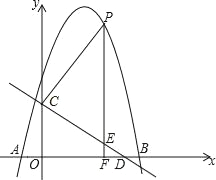
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于A(﹣1,0),B(5,0)兩點,直線y=﹣![]() x+3與y軸交于點C,與x軸交于點D.點P是直線CD上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
x+3與y軸交于點C,與x軸交于點D.點P是直線CD上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
(1)求拋物線的解析式;
(2)求PE的長最大時m的值.
(3)Q是平面直角坐標系內一點,在(2)的情況下,以PQCD為頂點的四邊形是平行四邊形是否存在?若存在,直接寫出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com