
【題目】如圖,已知A(-4,![]() ),B(-1,2)是一次函數y=kx+b與反比例函數y=
),B(-1,2)是一次函數y=kx+b與反比例函數y=![]() (m≠0,m<0)圖象的兩個交點,AC⊥x軸于C,BD⊥y軸于D。
(m≠0,m<0)圖象的兩個交點,AC⊥x軸于C,BD⊥y軸于D。

(1)根據圖象直接回答:在第二象限內,當x取何值時,一次函數大于反比例函數的值?
(2)求一次函數解析式及m的值;
(3)P是線段AB上的一點,連接PC,PD,若△PCA和△PDB面積相等,求點P坐標。
【答案】(1)、-4<x<-1;(2)、y=![]() ;m=-2;(3)、(
;m=-2;(3)、(![]() ,
,![]() ).
).
【解析】
試題分析:(1)、根據圖示直接得出答案;(2)、將A、B兩點坐標代入一次函數解析式求出k和b的值,將點B的坐標代入反比例函數解析式求出m的值;(3)、首先根據一次函數設出點P的坐標,求出AC、OC、BD、OD的長度,根據△PCA和△PDB的面積相等列出關于x的方程求出x的值,然后得出點P的坐標.
試題解析:(1)、由圖象,當-4<x<-1時,一次函數值大于反比例函數的值
(2)、把A(-4,![]() ),B(-1,2)代入y=kx+b得,
),B(-1,2)代入y=kx+b得, 解得:
解得:![]()
∴ 一次函數的解析式為y=![]()
把B(-1,2)代入y=![]() 得m=-2,即m的值為-2
得m=-2,即m的值為-2
(3)、設P的坐標為(x,![]() ),由A、B的坐標可知AC=
),由A、B的坐標可知AC=![]() ,OC=4,BD=1,OD=2,
,OC=4,BD=1,OD=2,
易知△PCA的高為x+4,△PDB的高2-(![]() ),由
),由![]() 可得
可得
![]() ,解得
,解得![]() ,此時
,此時![]()
∴ P點坐標為(![]() ,
,![]() )
)


科目:初中數學 來源: 題型:
【題目】下列判斷錯誤的是( )
A.兩組對邊分別相等的四邊形是平行四邊形
B.四個內角都相等的四邊形是矩形
C.四條邊都相等的四邊形是菱形
D.兩條對角線垂直且平分的四邊形是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
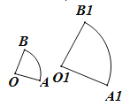
【題目】若兩個扇形滿足弧長的比等于它們半徑的比,則這稱這兩個扇形相似。如圖,如果扇形AOB與扇形![]() 是相似扇形,且半徑
是相似扇形,且半徑![]() (
(![]() 為不等于0的常數)那么下面四個結論:①∠AOB=∠
為不等于0的常數)那么下面四個結論:①∠AOB=∠![]() ;②△AOB∽△
;②△AOB∽△![]() ;③
;③![]() ;④扇形AOB與扇形
;④扇形AOB與扇形![]() 的面積之比為
的面積之比為![]() 。成立的個數為:( )
。成立的個數為:( )
A、1個 B、2個 C、3個 D、4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:直線l1與l2相交于點O,對于平面內任意一點M,點M到直線l1、l2的距離分別為p、q,則稱有序實數對(p,q)是點M的“距離坐標”,根據上述定義,“距離坐標”是(1,2)的點的個數是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com