
【題目】如圖,點A的坐標為(﹣4,0),點B的坐標為(0,﹣2),把點A繞點B順時針旋轉90°得到的點C恰好在拋物線y=ax2上,點P是拋物線y=ax2上的一個動點(不與點O重合),把點P向下平移2個單位得到動點Q,則:
(1)直接寫出AB所在直線的解析式、點C的坐標、a的值;
(2)連接OP、AQ,當OP+AQ獲得最小值時,求這個最小值及此時點P的坐標;
(3)是否存在這樣的點P,使得∠QPO=∠OBC,若不存在,請說明理由;若存在,請你直接寫出此時P點的坐標.

【答案】(1)a=![]() ;(2)OP+AQ的最小值為2
;(2)OP+AQ的最小值為2![]() ,此時點P的坐標為(﹣1,
,此時點P的坐標為(﹣1,![]() );(3)P(﹣4,8)或(4,8),
);(3)P(﹣4,8)或(4,8),
【解析】
(1)利用待定系數法求出直線AB解析式,根據旋轉性質確定出C的坐標,代入二次函數解析式求出a的值即可;
(2)連接BQ,可得PQ與OB平行,而PQ=OB,得到四邊形PQBO為平行四邊形,當Q在線段AB上時,求出OP+AQ的最小值,并求出此時P的坐標即可;
(3)存在這樣的點P,使得∠QPO=∠OBC,如備用圖所示,延長PQ交x軸于點H,設此時點P的坐標為(m,![]() m2),根據正切函數定義確定出m的值,即可確定出P的坐標.
m2),根據正切函數定義確定出m的值,即可確定出P的坐標.
(1)設直線AB解析式為y=kx+b,
把A(﹣4,0),B(0,﹣2)代入得:![]() ,
,
解得: ,
,
∴直線AB的解析式為y=﹣![]() x﹣2,
x﹣2,
根據題意得:點C的坐標為(2,2),
把C(2,2)代入二次函數解析式得:a=![]() ;
;
(2)連接BQ,

則易得PQ∥OB,且PQ=OB,
∴四邊形PQBO是平行四邊形,
∴OP=BQ,
∴OP+AQ=BQ+AQ≥AB=2![]() ,(等號成立的條件是點Q在線段AB上),
,(等號成立的條件是點Q在線段AB上),
∵直線AB的解析式為y=﹣![]() x﹣2,
x﹣2,
∴可設此時點Q的坐標為(t,﹣![]() t﹣2),
t﹣2),
于是,此時點P的坐標為(t,﹣![]() t),
t),
∵點P在拋物線y=![]() x2上,
x2上,
∴﹣![]() t=
t=![]() t2,
t2,
解得:t=0或t=﹣1,
∴當t=0,點P與點O重合,不合題意,應舍去,
∴OP+AQ的最小值為2![]() ,此時點P的坐標為(﹣1,
,此時點P的坐標為(﹣1,![]() );
);
(3)P(﹣4,8)或(4,8),
如備用圖所示,延長PQ交x軸于點H,

設此時點P的坐標為(m,![]() m2),
m2),
則tan∠HPO=![]() ,
,
又,易得tan∠OBC=![]() ,
,
當tan∠HPO=tan∠OBC時,可使得∠QPO=∠OBC,
于是,得![]() ,
,
解得:m=±4,
所以P(﹣4,8)或(4,8).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,AN∥CB,B、N在AC同側,BM、CN交于點D,AC=BC,且∠A+∠MDN=180°.
(1)如圖1,當∠NAC=90°,求證:BM=CN;
(2)如圖2,當∠NAC為銳角時,試判斷BM與CN關系并證明;
(3)如圖3,在(1)的條件下,且∠MBC=30°,一動點E在線段BM上運動過程中,連CE,將線段CE繞點C順時針旋轉90°至CF,取BE中點P,連AP、FP.設四邊形APFC面積為S,若AM=![]() ﹣1,MC=1,在E點運動過程中,請寫出S的取值范圍 .
﹣1,MC=1,在E點運動過程中,請寫出S的取值范圍 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在四邊形ABCD中,AC⊥BD于點E,AB=AC=BD,點M為BC中點,N為線段AM上的點,且MB=MN.

(1)求證:BN平分∠ABE;
(2)若BD=1,連結DN,當四邊形DNBC為平行四邊形時,求線段BC的長;
(3)如圖②,若點F為AB的中點,連結FN、FM,求證:△MFN∽△BDC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰![]() 中,
中,![]() ,D為BC的中點,過點C作
,D為BC的中點,過點C作![]() 于點G,過點B作
于點G,過點B作![]() 于點B,交CG的延長線于點F,連接DF交AB于點E.
于點B,交CG的延長線于點F,連接DF交AB于點E.
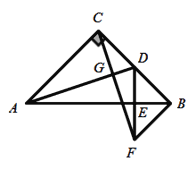
(1)求證:![]() ;
;
(2)求證:AB垂直平分DF;
(3)連接AF,試判斷![]() 的形狀,并說明理由.
的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場為了吸引顧客,設計了一種促銷活動:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”和“30元”的字樣.規定:顧客在本商場同一日內,每消費滿200元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回),商場根據兩小球所標金額的和返還相應價格的購物券,可以重新在本商場消費,某顧客剛好消費200元.
(1)該顧客至少可得到_____元購物券,至多可得到_______元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于30元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】你吃過拉面嗎?實際上在做拉面的過程中就滲透著數學知識:一定體積的面團做成拉面,面條的總長度![]() 是面條的粗細(橫截面積)
是面條的粗細(橫截面積)![]() 的反比例函數,其圖象如圖所示.
的反比例函數,其圖象如圖所示.

![]() 寫出
寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
![]() 求當面條粗總長度為
求當面條粗總長度為![]() 米時,面條的橫截面積是多少
米時,面條的橫截面積是多少![]() ?
?
![]() 求當要求面條的橫截面積不少于
求當要求面條的橫截面積不少于![]() 時,面條的總長度最多為多少米?
時,面條的總長度最多為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C是⊙O上一點,點P在直徑AB的延長線上,⊙O的半徑為3,PB=2,PC=4.
(1)求證:PC是⊙O的切線.
(2)求tan∠CAB的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D為直線BC上一動點(不與點B,C重合),在AD的右側作△ACE,使得AE=AD,∠DAE=∠BAC,連接CE.

(1)當D在線段![]() 上時.
上時.
①求證:![]() .
.
②請判斷點D在何處時,![]() ,并說明理由.
,并說明理由.
(2)當![]() 時,若
時,若![]() 中最小角為28°,求
中最小角為28°,求![]() 的度數.
的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com