
【題目】如圖,在平面直角坐標系中,點A在第一象限,點B(a,0),點C(0,b)分別在x軸,y軸上,其中a,b是二元一次方程![]() 的解,且a為不等式
的解,且a為不等式![]() 的最大整數解.
的最大整數解.
(1)證明:OB=OC;
(2)如圖1,連接AB,過點A作AD⊥AB交y軸于點D,在射線AD上截取AE=AB,連接CE,取CE的中點F,連接AF并延長至點G,使FG=AF,連接CG,OA.當點A在第一象限內運動(AD不經過點C)時,證明:∠OAF的大小不變;

科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC=5,cos∠ABC=0.6,將△ABC繞點C順時針旋轉,得到△A1B1C.
(1)如圖1,當點B1在線段BA延長線上時.①求證:BB1∥CA1;②求△AB1C的面積;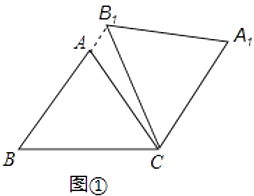
(2)如圖2,點E是BC邊的中點,點F為線段AB上的動點,在△ABC繞點C順時針旋轉過程中,點F的對應點是F1 , 求線段EF1長度的最大值與最小值的差.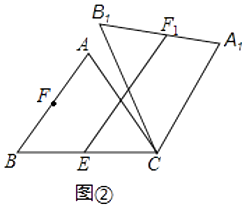
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為12cm的等邊三角形ABC中,點P從點A開始沿AB邊向點B以每秒鐘1cm的速度移動,點Q從點B開始沿BC邊向點C以每秒鐘2cm的速度移動.若P、Q分別從A、B同時出發,其中任意一點到達目的地后,兩點同時停止運動,求:
(1)經過6秒后,BP= cm,BQ= cm;
(2)經過幾秒后,△BPQ是直角三角形?
(3)經過幾秒△BPQ的面積等于![]() cm2?
cm2?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形網格中,小格的頂點叫做格點。小華按下列要求作圖:①在正方形網格的三條不同的實線上各取一個格點,使其中任意兩點不在同一條實線上;②連結三個格點,使之構成直角三角形。小華在左邊的正方形網格中作出了Rt⊿ABC。請你按照同樣的要求,在右邊的兩個正方形網格中各畫出一個直角三角形,并使三個網格中的直角三角形互不全等。



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,∠ABC的平分線交AC于點D,點O是AB上一點,⊙O過B、D兩點,且分別交AB,BC于點E,F.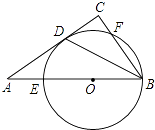
(1)求證:AC是⊙O的切線;
(2)已知AB=5,AC=4,求⊙O的半徑r.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某油箱容量為60L的汽車,加滿汽油后行駛了100km時,油箱中的汽油大約消耗了![]() ,如果加滿汽油后汽車行駛的路程為x(km),油箱中剩油量為y(L),則y與x之間的函數解析式和自變量取值范圍分別是( )
,如果加滿汽油后汽車行駛的路程為x(km),油箱中剩油量為y(L),則y與x之間的函數解析式和自變量取值范圍分別是( )
A. y=0.12x,x>0
B. y=60-0.12x,x>0
C. y=0.12x,0≤x≤500
D. y=60-0.12x,0≤x≤500
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC的三個頂點的位置如圖所示.現將△ABC平移,使得點A移至圖中的點A'的位置.
(1)平移后所得△ABC的頂點B的坐標為 ,C的坐標為 ;
(2)平移過程中△ABC掃過的面積為 ;
(3)將直線AB以每秒1個單位長度的速度向右平移,則平移 秒時該直線恰好經過點C.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題
(1)如圖1,AC和BD相交于點O,OA=OC,OB=OD,求證:DC∥AB.
(2)如圖2,在⊙O中,直徑AB=6,AB與弦CD相交于點E,連接AC、BD,若AC=2,求cosD的值.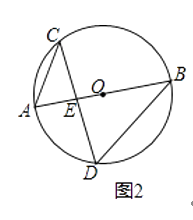
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com