
【題目】平面上,矩形ABCD與直徑為QP的半圓K如圖1擺放,分別延長DA和QP交于點O,且∠DOQ=60°,OQ=0D=3,OP=2,OA=AB=1.讓線段OD及矩形ABCD位置固定,將線段OQ連帶著半圓K一起繞著點O按逆時針方向開始旋轉,設旋轉角為α(0°≤α≤60°).
發現:
(1)當α=0°,即初始位置時,點P直線AB上.(填“在”或“不在”)求當α是多少時,OQ經過點B.
(2)在OQ旋轉過程中,簡要說明α是多少時,點P,A間的距離最小?并指出這個最小值;
(3)如圖2,當點P恰好落在BC邊上時,求a及S陰影
拓展:
如圖3,當線段OQ與CB邊交于點M,與BA邊交于點N時,設BM=x(x>0),用含x的代數式表示BN的長,并求x的取值范圍.
探究:當半圓K與矩形ABCD的邊相切時,求sinα的值.
【答案】
(1)在
(2)解:如圖2,連接AP,
∵OA+AP≥OP,
當OP過點A,即α=60°時,等號成立,
∴AP≥OP﹣OA=2﹣1=1,
∴當α=60°時,P、A之間的距離最小,
∴PA的最小值=1
(3)解:如圖2,
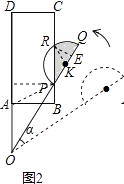
設半圓K與PC交點為R,連接RK,過點P作PH⊥AD于點H,
過點R作RE⊥KQ于點E,在Rt△OPH中,PH=AB=1,OP=2,
∴∠POH=30°,
∴α=60°﹣30°=30°,
∵AD∥BC,
∴∠RPO=∠POH=30°,
∴∠RKQ=2×30°=60°,
∴S扇形KRQ= ![]() =
= ![]() ,
,
在Rt△RKE中,RE=RKsin60°= ![]() ,
,
∴S△PRK= ![]() RE=
RE= ![]() ,∴S陰影=
,∴S陰影= ![]() +
+ ![]() ;
;
拓展:如圖5,
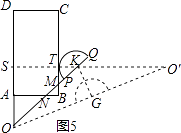
∵∠OAN=∠MBN=90°,∠ANO=∠BNM,
∴△AON∽△BMN,
∴ ![]() ,即
,即 ![]() ,
,
∴BN= ![]() ,
,
如圖4,
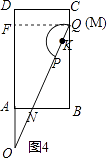
當點Q落在BC上時,x取最大值,作QF⊥AD于點F,BQ=AF= ![]() ﹣AO=2
﹣AO=2 ![]() ﹣1,
﹣1,
∴x的取值范圍是0<x≤2 ![]() ﹣1;
﹣1;
探究:半圓K與矩形ABCD的邊相切,分三種情況;
①如圖5,半圓K與BC相切于點T,設直線KT與AD,OQ的初始位置所在的直線分別交于點S,O′,
則∠KSO=∠KTB=90°,
作KG⊥OO′于G,在Rt△OSK中,
OS= ![]() =2,
=2,
在Rt△OSO′中,SO′=OStan60°=2 ![]() ,KO′=2
,KO′=2 ![]() ﹣
﹣ ![]() ,
,
在Rt△KGO′中,∠O′=30°,
∴KG= ![]() KO′=
KO′= ![]() ﹣
﹣ ![]() ,
,
∴在Rt△OGK中,sinα= ![]() =
= ![]() =
= ![]() ,
,
②當半圓K與AD相切于T,如圖6,
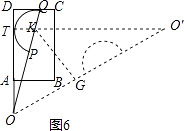
同理可得sinα= 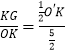 =
= 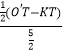 =
= ![]() =
= ![]() ;
;
③當半圓K與CD切線時,點Q與點D重合,且為切點,
∴α=60°,
∴sinα=sin60 ![]() ,
,
綜上所述sinα的值為: ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】解:發現:(1)在,
當OQ過點B時,在Rt△OAB中,AO=AB,
∴∠DOQ=∠ABO=45°,
∴α=60°﹣45°=15°;
(1)在,當OQ過點B時,在Rt△OAB中,AO=AB,得到∠DOQ=∠ABO=45°,求得α=60°﹣45°=15°;(2)如圖2,連接AP,由OA+AP≥OP,當OP過點A,即α=60°時,等號成立,于是有AP≥OP﹣OA=2﹣1=1,當α=60°時,P、A之間的距離最小,即可求得結果(3)如圖2,設半圓K與PC交點為R,連接RK,過點P作PH⊥AD于點H,過點R作RE⊥KQ于點E,在Rt△OPH中,PH=AB=1,OP=2,得到∠POH=30°,求得α=60°﹣30°=30°,由于AD∥BC,得到∠RPO=∠POH=30°,求出∠RKQ=2×30°=60°,于是得到結果;
拓展:如圖5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN求出BN= ![]() ,如圖4,當點Q落在BC上時,x取最大值,作QF⊥AD于點F,BQ=AF=
,如圖4,當點Q落在BC上時,x取最大值,作QF⊥AD于點F,BQ=AF= ![]() ﹣AO=2
﹣AO=2 ![]() ﹣1,求出x的取值范圍是0<x≤2
﹣1,求出x的取值范圍是0<x≤2 ![]() ﹣1;
﹣1;
探究:半圓K與矩形ABCD的邊相切,分三種情況;
①如圖5,半圓K與BC相切于點T,設直線KT與AD,OQ的初始位置所在的直線分別交于點S,O′,于是得到∠KSO=∠KTB=90°,作KG⊥OO′于G,在Rt△OSK中,求出OS= ![]() =2,在Rt△OSO′中,SO′=OStan60°=2
=2,在Rt△OSO′中,SO′=OStan60°=2 ![]() ,KO′=2
,KO′=2 ![]() ﹣
﹣ ![]() 在Rt△KGO′中,∠O′=30°,求得KG=
在Rt△KGO′中,∠O′=30°,求得KG= ![]() KO′=
KO′= ![]() ﹣
﹣ ![]() ,在Rt△OGK中,求得結果;②當半圓K與AD相切于T,圖6,同理可得sinα的值③當半圓K與CD切線時,點Q與點D重合,且為切點,得到α=60°于是結論可求.
,在Rt△OGK中,求得結果;②當半圓K與AD相切于T,圖6,同理可得sinα的值③當半圓K與CD切線時,點Q與點D重合,且為切點,得到α=60°于是結論可求.


科目:初中數學 來源: 題型:
【題目】一個不透明的布袋里裝有3個球,其中2個紅球,1個白球,它們除顏色外其余都相同.
(1)摸出1個球,記下顏色后放回,并攪勻,再摸出1個球,求兩次摸出的球恰好顏色不同的概率(請用“畫樹狀圖”或“列表”等方法寫出分析過程);
(2)現再將n個白球放入布袋,攪勻后,使摸出1個球是白球的概率為 ![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前,步行已成為人們最喜愛的健身方法之一,通過手機可以計算行走的步數與相應的能量消耗.對比手機數據發現小明步行12 000步與小紅步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步數比小紅多10步,求小紅每消耗1千卡能量需要行走多少步?
【答案】小紅每消耗1千卡能量需要行走30步.
【解析】分析:設小紅每消耗1千卡能量需要行走x步,則小明每消耗1千卡能量需要行走(x+10)步,根據數量關系消耗能量千卡數=行走步數÷每消耗1千卡能量需要行走步數結合小明步行12000步與小紅步行9000步消耗的能量相同,即可得出關于x的分式方程,解之后經檢驗即可得出結論.
詳解:設小紅每消耗1千卡能量需要行走x步,則小明每消耗1千卡能量需要行走(x+10)步,
根據題意,得
![]() ,
,
解得x=30.
經檢驗:x=30是原方程的解.
答:小紅每消耗1千卡能量需要行走30步.
點睛:本題考查了分式方程的應用,根據數量關系消耗能量千卡數=行走步數÷每消耗1千卡能量需要行走步數列出關于x的分式方程是解題的關鍵.
【題型】解答題
【結束】
25
【題目】如圖,在△ABC中,AD是BC邊上的中線,E是AD的中點,過點A作BC的平行線交BE的延長線于F,連接CF.
(1)求證:四邊形ADCF是平行四邊形;
(2)當△ABC滿足什么條件時,四邊形ADCF為正方形,請你添加適當的條件并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的頂點A,B與正方形EFGH的頂點G,H同在一段拋物線上,且拋物線的頂點同時落在CD和y軸上,正方形邊AB與EF同時落在x軸上,若正方形ABCD的邊長為4,則正方形EFGH的邊長為 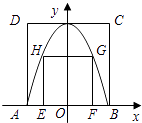
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點M,與BD相交于點N,連接BM,DN.

(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,正方形ABCD與正方形AEFG的邊AB,AE(AB<AE)在一條直線上,正方形AEFG以點A為旋轉中心逆時針旋轉,設旋轉角為α.在旋轉過程中,兩個正方形只有點A重合,其它頂點均不重合,連接BE,DG.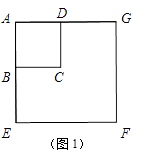
(1)當正方形AEFG旋轉至如圖2所示的位置時,求證:BE=DG;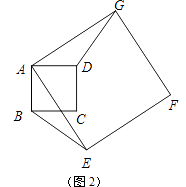
(2)如圖3,如果α=45°,AB=2,AE=3 ![]() .
.
①求BE的長;②求點A到BE的距離;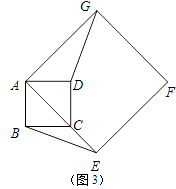
(3)當點C落在直線BE上時,連接FC,直接寫出∠FCD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明遇到下面的問題:求代數式![]() 的最小值并寫出取到最小值時的x值.經過觀察式子結構特征,小明聯想到可以用解一元二次方程中的配方法來解決問題,具體分析過程如下:
的最小值并寫出取到最小值時的x值.經過觀察式子結構特征,小明聯想到可以用解一元二次方程中的配方法來解決問題,具體分析過程如下:
![]() ,所以,當x=1 時,代數式有最小值是-4.
,所以,當x=1 時,代數式有最小值是-4.
(1)請你用上面小明思考問題的方法解決下面問題.
① ![]() 的最小值是_______;②求
的最小值是_______;②求![]() 的最小值.
的最小值.
(2)小明受到上面問題的啟發,自己設計了一個問題,并給出解題過程及結論如下:
問題:當x為實數時,求![]() 的最小值.
的最小值.
解:![]() ,∴原式有最小值是5.
,∴原式有最小值是5.
請你判斷小明的結論是否正確,并簡要說明理由.
判斷:__________,理由:____________________________________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com