
【題目】已知函數y1=x(x≥0),y2=![]() (x>0)的圖象如圖所示,則以下結論:
(x>0)的圖象如圖所示,則以下結論:
①兩函數圖象的交點A的坐標為(2,2);②當x>2時,y1>y2;
③BC=2;④兩函數圖象構成的圖形是軸對稱圖形;
⑤當x逐漸增大時,y1隨著x的增大而增大,y2隨著x的增大而減小.
其中正確結論的序號是____________.

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】八(2)班組織了一次經典誦讀比賽,甲、乙兩隊各10人的比賽成績如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲隊成績的中位數是 分,乙隊成績的眾數是 分;
(2)計算乙隊的平均成績和方差;
(3)已知甲隊成績的方差是1.4,則成績較為整齊的是 隊.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,O為正方形對角線的交點,BE平分∠DBC,交DC于點E,延長BC到點F,使CF=CE,連結DF,交BE的延長線于點G,連結OG.
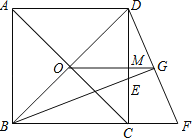
(1)求證:△BCE≌△DCF.
(2)判斷OG與BF有什么關系,證明你的結論.
(3)若DF2=8-4![]() ,求正方形ABCD的面積?
,求正方形ABCD的面積?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】概念學習
規定:求若干個相同的有理數(均不等于0)的除法運算叫做除方,例如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.類比有理數的乘方,我們把2÷2÷2記作2③,讀作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)記作(﹣3)④,讀作“﹣3的圈4次方”,一般地,把![]() (a≠0)記作
(a≠0)記作![]() a
a![]() ,讀作“a的圈n次方”.
,讀作“a的圈n次方”.
初步探究
(1)直接寫出計算結果:2③=________,![]() =________;
=________;
(2)關于除方,下列說法錯誤的是________
A.任何非零數的圈2次方都等于1; B.對于任何正整數n,1![]() =1;
=1;
C.3④=4③ ; D.負數的圈奇數次方結果是負數,負數的圈偶數次方結果是正數.
深入思考
我們知道,有理數的減法運算可以轉化為加法運算,除法運算可以轉化為乘法運算,有理數的除方運算如何轉化為乘方運算呢?

(1)試一試:仿照上面的算式,將下列運算結果直接寫成冪的形式.
(﹣3)④=________;5⑥=________;![]() =________.
=________.
(2)想一想:將一個非零有理數a的圈n次方寫成冪的形式等于________;
(3)算一算:24÷23+(-16)×2④.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠倉庫儲存了部分原料,按原計劃每時消耗2 t,可用60 h.由于技術革新,實際生產能力有所提高,即每時消耗的原料量大于計劃消耗的原料量.設現在每時消耗原料x(單位:t),庫存的原料可使用的時間為y(單位:h).
(1)寫出y關于x的函數解析式,并求出自變量的取值范圍;
(2)若恰好經過24 h才有新的原料進廠,為了使機器不停止運轉,則x應控制在什么范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
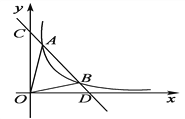
【題目】如圖,一次函數y=kx+b與反比例函數y=![]() (x>0)的圖象交于A(m,6),B(3,n)兩點.
(x>0)的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數的解析式;
(2)根據圖象直接寫出kx+b-![]() <0時x的取值范圍;
<0時x的取值范圍;
(3)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當m為何值時,關于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有兩個不相等的實數根;
(2)有兩個相等的實數根;
(3)沒有實數根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com