
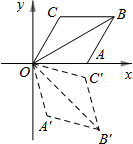
 如圖,已知菱形OABC的一邊OA在x軸上,OA∥BC,OC∥AB,且OA=AB=BC=CO,將菱形OABC變換到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,則點B′的坐標為( )
如圖,已知菱形OABC的一邊OA在x軸上,OA∥BC,OC∥AB,且OA=AB=BC=CO,將菱形OABC變換到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,則點B′的坐標為( )| A. | (3,$\sqrt{3}$) | B. | (3,-$\sqrt{3}$) | C. | ($\sqrt{6}$,$\sqrt{6}$) | D. | ($\sqrt{6}$,-$\sqrt{6}$) |
分析 首先根據菱形的性質,即可求得∠AOB的度數,又由將菱形OABC繞原點O順時針旋轉75°至OA′B′C′的位置,可求得∠B′OA的度數,然后在Rt△B′OF中,利用三角函數即可求得OF與B′F的長,則可得點B′的坐標.
解答 解:過點B作BE⊥OA于E,過點B′作B′F⊥OA于F,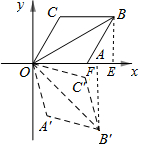
∴∠BE0=∠B′FO=90°,
∵四邊形OABC是菱形,
∴OA∥BC,∠AOB=$\frac{1}{2}$∠AOC,
∴∠AOC+∠C=180°,
∵∠C=120°,
∴∠AOC=60°,
∴∠AOB=30°,
∵菱形OABC繞原點O順時針旋轉75°至OA′B′C′的位置,
∴∠BOB′=75°,OB′=OB=2$\sqrt{3}$,
∴∠B′OF=45°,
在Rt△B′OF中,
OF=OB′•cos45°=2$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=$\sqrt{6}$,
∴B′F=$\sqrt{6}$,
∴點B′的坐標為:($\sqrt{6}$,-$\sqrt{6}$).
故選:D.
點評 此題考查了平行四邊形的性質,旋轉的性質以及直角三角形的性質與三角函數的性質等知識.此題綜合性較強,難度適中,解題的關鍵是注意數形結合思想的應用.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:解答題
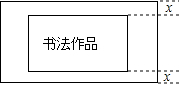 如圖,現有一幅書法作品(圖中陰影部分所示)需要裝裱,已知該書法作品的長為50cm,寬為30cm,上、下邊襯等寬、左、右邊襯等寬,并且上、下邊襯的寬與左、右邊襯的寬比為1:2,已知裝裱后的作品的面積為2800cm2.
如圖,現有一幅書法作品(圖中陰影部分所示)需要裝裱,已知該書法作品的長為50cm,寬為30cm,上、下邊襯等寬、左、右邊襯等寬,并且上、下邊襯的寬與左、右邊襯的寬比為1:2,已知裝裱后的作品的面積為2800cm2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{5}{12}$ | B. | $-\frac{5}{12}$ | C. | $-\frac{12}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com