【題目】為了從甲、乙兩名射擊運動員中選拔一名參加比賽，對這兩名運動員進行測試，他們10次射擊命中的環數如下：
甲 | 7 | 9 | 8 | 6 | 10 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 | 6 | 8 | 9 | 7 | 10 |
根據測試成績，你認為選擇哪一名運動員參賽更好？為什么？
【答案】選擇乙運動員參賽更好．理由見解析．
【解析】
試題分析：先計算甲乙的平均數，再根據方程公式計算甲乙的方差，然后通過比較方差的大小，根據方差的意義決定選擇哪一名運動員參賽更好．
試題解析：
=
（7+9+8+6+10+7+9+8+6+10）=8（環），
=（7+8+9+8+8+6+8+9+7+10）=8（環），
S甲2= [（7-8）2+（9-8）2+（8-8）2+（6-8）2+（10-8）2+（7-8）2+（9-8）2+（8-8）2+（6-8）2+（10-8）2]=2，
S乙2=
[（7-8）2+（8-8）2+（9-8）2+（8-8）2+（8-8）2+（6-8）2+（8-8）2+（9-8）2+（7-8）2+（10-8）2]=1．2，
∵S甲2＞S乙2，
∴乙運動員的成績比較穩定，
∴選擇乙運動員參賽更好．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
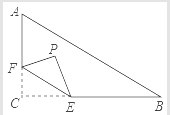
【題目】如圖，在Rt△ABC中，∠C=90°，AC=6，BC=8，點F在邊AC上，點E為邊BC上的動點，將△CEF沿直線EF翻折，點C落在點P處，若點P能落在線段AB上，則線段CF長的最小值是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點A，B的坐標分別為（－1，0），（3，0），現同時將點A，B分別向上平移2個單位，再向右平移1個單位，分別得到點A，B的對應點C，D，連接AC，BD，CD．
（1）求點C，D的坐標及平行四邊形ABDC的面積
.
（2）在y軸上是否存在一點P，連接PA，PB，使
＝2，若存在這樣一點，求出點P的坐標，若不存在，試說明理由．
（3）點P是四邊形ABCD邊上的點，若△OPC為等腰三角形時，直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
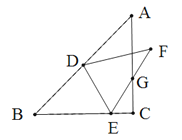
【題目】如圖，△ABC中，∠ACB=90°，AB=2，BC=AC，D為AB的中點，E為BC上一點，將△BDE沿DE翻折，得到△FDE，EF交AC于點G，則△ECG的周長是___________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在△ABC中，AB=AC，點D是BC的中點，點E在AD上．
（1）求證：BE=CE；
（2）如圖2，若BE的延長線交AC于點F，且BF⊥AC，垂足為F，∠BAC=45°，原題設其它條件不變．求證：△AEF≌△BCF．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在某中學第八屆校園文化藝術節中，其中有三個年級老師參加的“校園歌手大獎賽”，藝術節組委會要求三個年級先進行預賽，選出男、女各一名選手參加決賽，七、八、九年級選手編號分別為男1號，女1號；男2號，女2號；男3號，女3號，比賽規則是男女各一人組成搭檔進行決賽比賽．
（1）求是同一年級男、女教師選手組成搭檔的概率．
（2）求低年級男教師與高年級女教師組成搭檔的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一個直角三角形紙片OAB，其中∠AOB=90°，OA=2，OB=4．如圖，將該紙片放置在平面直角坐標系中，折疊該紙片，折痕與邊OB交于點C，與邊AB交于點D．
（1）若折疊后使點B與點A重合，求點C的坐標．
（2）若折疊后點B落在邊OA上的點為B′，是否存在點B′，使得四邊形BCB′D是菱形？若存在，請說明理由并求出菱形的邊長；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠CAB=70°，將△ABC繞點A逆時針旋轉到△AB′C′的位置，使得CC′∥AB，則∠BAB′的度數是（ ）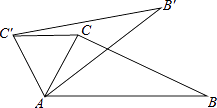 
A.70°
B.35°
C.40°
D.50°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
