
【題目】在平面直角坐標(biāo)系中,A(2,0)、B(0,3),過點(diǎn)B作直線l∥x軸,點(diǎn)P(a,3)是直線上的動點(diǎn),以AP為邊在AP右側(cè)作等腰RtAPQ,∠APQ=90°,直線AQ交y軸于點(diǎn)C.
(1)當(dāng)a=![]() 時,求點(diǎn)Q的坐標(biāo);
時,求點(diǎn)Q的坐標(biāo);
(2)當(dāng)PA+PO最小時,求a.

【答案】(1)(4.5,3.5);(2)a=1
【解析】試題分析:(1)要求點(diǎn)Q的坐標(biāo),可作QF⊥BP,由于BP、OB已知,只需求出PF和QF.從條件“△APQ為等腰直角三角形”出發(fā),構(gòu)造全等,即可解決問題.
(2)本題要求動點(diǎn)P到兩定點(diǎn)A、O的距離之和AP+OP的最小值,只需找到點(diǎn)O關(guān)于直線l的對稱點(diǎn)M,連接AM,AM與直線l的交點(diǎn)即為滿足條件的點(diǎn)P,就可求出a的值.
試題解析:(1)過點(diǎn)P作PE⊥OA,垂足為E,過點(diǎn)Q作QF⊥BP,垂足為F,如圖1,
∵BP∥OA,PE⊥OA,∴∠EPF=∠PEO=90°,
∵∠APQ=90°,∴∠EPA=∠FPQ=90°-∠APF,
在△PEA和△PFQ中,  ,∴△PEA≌△PFQ,
,∴△PEA≌△PFQ,
∴PE=PF,EA=QF,
∵a=1,∴P(1,3),∴OE=BP=1,PE=3,
∵A(2,0),∴OA=2,∴EA=1,∴PF=3,QF=1,
∴點(diǎn)Q的坐標(biāo)為(4,4);
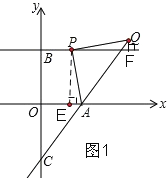
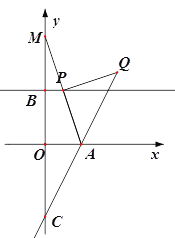
(2)如圖,作點(diǎn)O關(guān)于直線l 的對稱點(diǎn)M,連接AM,交直線l于點(diǎn)P,則此時OP+OA的值最小,
由題意易用得點(diǎn)M的坐標(biāo)為(0,6),
設(shè)直線AM的解析式為y=kx+b,
則有![]() ,解得
,解得![]() ,所以直線AM的解析式為:y=-3x+6,
,所以直線AM的解析式為:y=-3x+6,
當(dāng)y=3時,3=-3x+6,解得x=1,所以點(diǎn)P坐標(biāo)為(1,3),所以a=1.


 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,兩條互相平行的河岸,在河岸一邊測得AB為20米,在另一邊測得CD為70米,用測角器測得∠ACD=30°,測得∠BDC=45°,求兩條河岸之間的距離.(![]() ,
, ![]() ≈1.7,結(jié)果保留整數(shù))
≈1.7,結(jié)果保留整數(shù))

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】資料:小球沿直線撞擊水平格檔反彈時(不考慮垂直撞擊),撞擊路線與水平格檔所成的銳角等于反彈路線與水平格檔所成的銳角.以圖(1)為例,如果黑球 ![]() 沿從
沿從 ![]() 到
到 ![]() 方向在
方向在 ![]() 點(diǎn)處撞擊
點(diǎn)處撞擊 ![]() 邊后將沿從
邊后將沿從 ![]() 到
到 ![]() 方向反彈,根據(jù)反彈原則可知
方向反彈,根據(jù)反彈原則可知 ![]() ,即
,即 ![]() .如圖(2)和(3),
.如圖(2)和(3),![]() 是一個長方形的彈子球臺面,有黑白兩球
是一個長方形的彈子球臺面,有黑白兩球 ![]() 和
和 ![]() ,小球沿直線撞擊各邊反彈時遵循資料中的反彈原則.(回答以下問題時將黑白兩球均看作幾何圖形中的點(diǎn),不考慮其半徑大小)
,小球沿直線撞擊各邊反彈時遵循資料中的反彈原則.(回答以下問題時將黑白兩球均看作幾何圖形中的點(diǎn),不考慮其半徑大小)

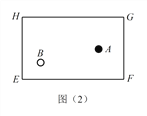

(1)探究(1):黑球 ![]() 沿直線撞擊臺邊
沿直線撞擊臺邊 ![]() 哪一點(diǎn)時,可以使黑球
哪一點(diǎn)時,可以使黑球 ![]() 經(jīng)臺邊
經(jīng)臺邊 ![]() 反彈一次后撞擊到白球
反彈一次后撞擊到白球 ![]() ?請?jiān)趫D(2)中畫出黑球
?請?jiān)趫D(2)中畫出黑球 ![]() 的路線圖,標(biāo)出撞擊點(diǎn),并簡單證明所作路線是否符合反彈原則.
的路線圖,標(biāo)出撞擊點(diǎn),并簡單證明所作路線是否符合反彈原則.
(2)探究(2):黑球 ![]() 沿直線撞擊臺邊
沿直線撞擊臺邊 ![]() 哪一點(diǎn)時,可以使黑球
哪一點(diǎn)時,可以使黑球 ![]()
![]() 反彈一次后,再撞擊臺邊
反彈一次后,再撞擊臺邊 ![]() 反彈一次撞擊到白球
反彈一次撞擊到白球 ![]() ?請?jiān)趫D(3)中畫出黑球
?請?jiān)趫D(3)中畫出黑球 ![]() 的路線圖,標(biāo)出黑球撞擊
的路線圖,標(biāo)出黑球撞擊 ![]() 邊的撞擊點(diǎn),簡單說明作法,不用證明.
邊的撞擊點(diǎn),簡單說明作法,不用證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線AB分別交y軸、x軸于A、B兩點(diǎn),OA=2,tan∠ABO=0.5,拋物線y=﹣x2+bx+c過A、B兩點(diǎn).
(1)求直線AB和這個拋物線的解析式;
(2)設(shè)拋物線的頂點(diǎn)為D,求△ABD的面積;
(3)作垂直x軸的直線x=t,在第一象限交直線AB于M,交這個拋物線于N.求當(dāng)t取何值時,MN的長度L有最大值?最大值是多少?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠ACB=90![]() ,D為BC邊上的中點(diǎn),DE⊥AB,垂足為點(diǎn)E,過點(diǎn)B作BF∥AC交DE的延長線于點(diǎn)F,連接CF.
,D為BC邊上的中點(diǎn),DE⊥AB,垂足為點(diǎn)E,過點(diǎn)B作BF∥AC交DE的延長線于點(diǎn)F,連接CF.
(1)求證:AD⊥CF;
(2)連接AF,試判斷△ACF的形狀,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】證明定理:三角形三條邊的垂直平分線相交于一點(diǎn),并且這一點(diǎn)到三個頂點(diǎn)的距離相等,已知:
如圖,在△ABC中,分別作AB邊、BC邊的垂直平分線,兩線相交于點(diǎn)P,分別交AB邊、BC邊于點(diǎn)E、F.
求證:AB、BC、AC的垂直平分線相交于點(diǎn)P
證明:∵點(diǎn)P是AB邊垂直平線上的一點(diǎn),
∴ = ( ).
同理可得,PB= .
∴ = (等量代換).
∴ (到一條線段兩個端點(diǎn)距離相等的點(diǎn),在這條線段的 )
∴AB、BC、AC的垂直平分線 .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com