
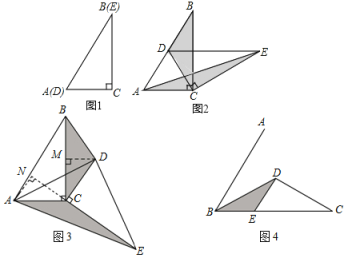
【題目】如圖1,將兩個完全相同的三角形紙片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
(1)操作發現
如圖2,固定![]() ,使
,使![]() 繞點
繞點![]() 旋轉,當點
旋轉,當點![]() 恰好落在
恰好落在![]() 邊上時,填空:
邊上時,填空:
①線段![]() 與
與![]() 的位置關系是______;
的位置關系是______;
②設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的數量關系是______
的數量關系是______
(2)猜想論證
當![]() 繞點
繞點![]() 旋轉到如圖3所示的位置時,小明猜想1.中
旋轉到如圖3所示的位置時,小明猜想1.中![]() 與
與![]() 的數量關系仍然成立,并嘗試分別作出了
的數量關系仍然成立,并嘗試分別作出了![]() 和
和![]() 中
中![]() 、
、![]() 邊上的高,請你證明小明的猜想.
邊上的高,請你證明小明的猜想.
(3)拓展探究
已知∠ABC=60°,點![]() 是角平分線上一點,
是角平分線上一點,![]() ,
,![]() 交
交![]() 于點
于點![]() (如圖4).若在射線
(如圖4).若在射線![]() 上存在點
上存在點![]() ,使
,使![]() ,請求出相應的
,請求出相應的![]() 的長.
的長.
【答案】(1)操作發現:①DE∥AC;②![]() =
=![]() ;(2)猜想論證:
;(2)猜想論證:![]() =
=![]() 仍然成立,證明見解析;(3)拓展探究:
仍然成立,證明見解析;(3)拓展探究:![]() =
=![]() 或
或![]()
【解析】
(1)操作發現:①根據直角三角形的性質即可求出∠EDC,然后證出△CAD為等邊三角形可得∠DCA=60°,從而得出∠EDC=∠DCA,然后根據平行線的判定即可得出結論;
②根據平行線之間的距離處處相等和同底等高可得S△DAC=![]() ,然后根據30°所對的直角邊是斜邊的一半和等邊三角形的性質可得點D為AB的中點,從而證出S△DAC=
,然后根據30°所對的直角邊是斜邊的一半和等邊三角形的性質可得點D為AB的中點,從而證出S△DAC=![]() ,即可得出結論;
,即可得出結論;
(2)猜想論證:利用AAS證出△ACN≌△DCM,即可得出AN=DM,然后根據旋轉的性質可得EC=BC,然后根據兩個三角形等底等高即可得出結論;
(3)拓展探究:延長CD交AB于點H,過點E作EG⊥BD于G,利用30°所對的直角邊是斜邊的一半和勾股定理分別求出BH和GE,然后根據點F的位置分類討論,根據兩個三角形的面積相等、底相等那么高也相等即可求出FH,從而分別求出BF的長
解:(1)操作發現:①DE∥AC,理由如下:
∵![]() ,
,![]() .
.
∴∠BAC=90°-∠B=60°,∠EDC=90°-∠DEC=60°
∵點![]() 恰好落在
恰好落在![]() 邊上時,
邊上時,
∴CA=CD
∴△CAD為等邊三角形
∴∠DCA=60°
∴∠EDC=∠DCA
∴DE∥AC
故答案為:DE∥AC.
②![]() =
=![]() ,理由如下
,理由如下
∵DE∥AC
根據平行線之間的距離處處相等
∴S△DAC=![]()
在Rt△ABC中,∠B=30°
∴AB=2AC
∵△CAD為等邊三角形
∴AC=AD
∴AB=2AD
∴點D為AB的中點
∴S△DAC=![]()
∴![]() =
=![]()
故答案為:![]() =
=![]() .
.
(2)猜想論證:![]() =
=![]() 仍然成立,證明如下
仍然成立,證明如下
∵AN、DM分別是△ACE、△BCD邊上的高
∴∠ANC=∠DMC=90°
∵∠ACN+∠NCB=90°,∠DCM+∠NCB=90°
∴∠ACN=∠DCM
在△ACN和△DCM中
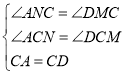
∴△ACN≌△DCM
∴AN=DM
∵EC=BC
∴△ACE和△BCD等底等高
∴![]() =
=![]()
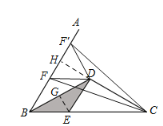
(3)拓展探究:延長CD交AB于點H,過點E作EG⊥BD于G,
∵∠ABC=60°,點![]() 是角平分線上一點,
是角平分線上一點,![]() ,
,
∴∠HBD=∠CBD=![]() ∠ABC=30°
∠ABC=30°
∵![]()
∴∠DCB=∠DBC=30°
∴∠BHC=180°-∠HBC-∠DCB=90°
在Rt△BDH中,HD=![]() ,BH=
,BH=![]()
∵![]()
∴∠EDB=∠HBD=30°
∴∠EBD=∠EDB
∴EB=ED
∴BG=![]() =2
=2
在Rt△BEG中,設GE=x,BE=2GE=2x
根據勾股定理可得:GE2+BG2=BE2
即x 2+22=(2x)2
解得:x=![]()
∴GE=![]()
(i)當點F在線段BH上時,
∵![]() ,
,![]()
∴FH=GE=![]()
∴BF=BH-FH=![]() ;
;
(ii)當![]() 在線段BH的延長線上時
在線段BH的延長線上時
同理可得![]() H= GE=
H= GE=![]()
∴B![]() =BH+
=BH+![]() H=
H=![]()
綜上所述:![]() =
=![]() 或
或![]()


科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象開口向上,圖象經過點(﹣1,2)和(1,0),且與y軸相交于負半軸,給出五個結論:①a+b+c=0,②abc<0,③2a+b>0,④a+c=1,⑤當﹣1<x<1時,y<0;其中正確的結論的序號( )
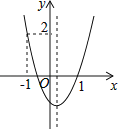
A.①③⑤B.②③④C.①③④D.②③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
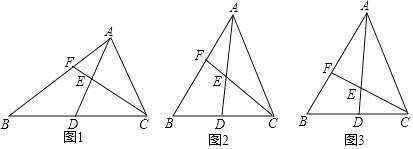
【題目】在△ABC中,AD為BC邊上的中線,E為AD上一動點,設DE=nEA,連接CE并延長,交AB于點F.
(1)嘗試探究:如圖1,當∠BAC=90°,∠B=30°,DE=EA時,BF,BA之間的數量關系是 ;
(2)類比延伸:如圖2,當△ABC為銳角三角形,DE=EA時,(1)中的結論是否仍然成立?若成立,請給予證明;若不成立,請說明理由;
(3)拓展遷移:如圖3,當△ABC為銳角三角形,DE=nEA時,請直接寫出BF,BA之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學準備舉辦一次演講比賽,每班限定兩人報名,初三(1)班的三位同學(兩位女生,一位男生)都想報名參加,班主任李老師設計了一個摸球游戲,利用已學過的概率知識來決定誰去參加比賽,游戲規則如下:在一個不透明的箱子里放3個大小質地完全相同的乒乓球,在這3個乒乓球上分別寫上![]() 、
、![]() 、
、![]() (每個字母分別代表一位同學,其中
(每個字母分別代表一位同學,其中![]() 、
、![]() 分別代表兩位女生,
分別代表兩位女生,![]() 代表男生),攪勻后,李老師從箱子里隨機摸出一個乒乓球,不放回,再次攪勻后隨機摸出第二個乒乓球,根據乒乓球上的字母決定誰去參加比賽。
代表男生),攪勻后,李老師從箱子里隨機摸出一個乒乓球,不放回,再次攪勻后隨機摸出第二個乒乓球,根據乒乓球上的字母決定誰去參加比賽。
(1)求李老師第一次摸出的乒乓球代表男生的概率;
(2)請用列表或畫樹狀圖的方法求恰好選定一名男生和一名女生參賽的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校園安全”受到全社會的廣泛關注,某中學對部分學生就校園安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了下面兩幅尚不完整的統計圖,請根據統計圖中所提供的信息解答下列問題:
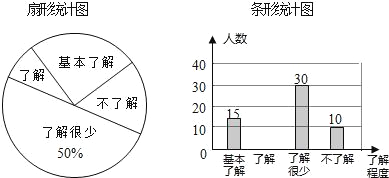
(1)接受問卷調查的學生共有 人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為 度;
(2)請補全條形統計圖;
(3)若該中學共有學生900人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() 是
是![]() 的外接圓,
的外接圓,![]() 是直徑,
是直徑,![]() 是
是![]() 外一點且滿足
外一點且滿足![]() ,連接
,連接![]() .
.
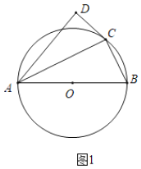
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的長;
的長;
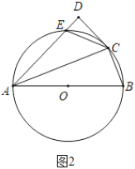
(3)如圖2,當![]() 時,
時,![]() 與
與![]() 交于
交于![]() 點,試寫出
點,試寫出![]() 、
、![]() 、
、![]() 之間的數量關系并證明.
之間的數量關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC和△CDE都是等腰三角形,∠BAC=∠EDC=120°.
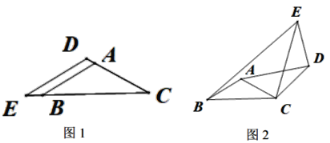
(1)如圖1,A、D、C在同一直線上時,![]() =_______,
=_______,![]() =_______;
=_______;
(2)在圖1的基礎上,固定△ABC,將△CDE繞C旋轉一定的角度α(0°<α<360°),如圖2,連接AD、BE.
① ![]() 的值有沒有改變?請說明理由.
的值有沒有改變?請說明理由.
②拓展研究:若AB=1,DE=![]() ,當 B、D、E在同一直線上時,請計算線段AD的長;
,當 B、D、E在同一直線上時,請計算線段AD的長;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在△ABC中,AB=AC,點D是AB上一點,以BD為直徑的⊙0與AC邊相切于點E,交BC于點F,FG⊥AC于點G.
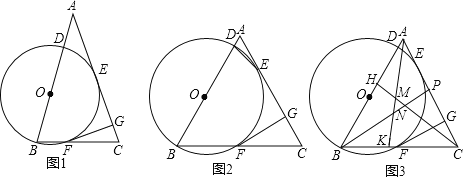
(1)如圖l,求證:GE=GF;
(2)如圖2,連接DE,∠GFC=2∠AED,求證:△ABC為等邊三角形;
(3)如圖3,在(2)的條件下,點H、K、P分別在AB、BC、AC上,AK、BP分別交CH于點M、N,AH=BK,∠PNC﹣![]() ∠BAK=60°,CN=6,CM=4
∠BAK=60°,CN=6,CM=4![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com