
【題目】如圖,直線L1∥L2 , 圓O與L1和L2分別相切于點A和點B,點M和點N分別是L1和L2上的動點,MN沿L1和L2平移,圓O的半徑為1,∠1=60°,當MN與圓相切時,AM的長度等于 . 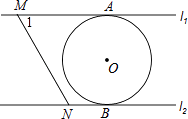
【答案】![]() 或
或 ![]()
【解析】解: 當MN在左側與⊙O相切時,連接OM、OA,如圖1,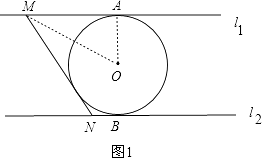
∵MA、MN是⊙O的切線,
∴OM平分∠AMN,OA⊥MA,
∴∠AMO=30°,
∴OM=2OA=2,
在Rt△OAM中,MA= ![]() =
= ![]() ;
;
當MN在右側與⊙O相切時,連接OM、OA,如圖2,
∵∠1=60°,
∴∠AMN=120°,
同上可知∠AMO= ![]() ∠AMN=60°,
∠AMN=60°,
∴OM=2AM,
在Rt△OAM中,MA2=OM2﹣OA2 , 即MA2=4MA2﹣1,解得MA= ![]() ;
;
綜上可知MA的長度為 ![]() 或
或 ![]() ,
,
所以答案是: ![]() 或
或 ![]() .
.
【考點精析】關于本題考查的平行線的性質和切線的性質定理,需要了解兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補;切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為原點,直線AB分別與x軸、y軸交于點B和A,與反比例函數的圖象交于C、D,CE⊥x軸于點E,若tan∠ABO= ![]() ,OB=4,OE=2,點D的坐標為(6,m).
,OB=4,OE=2,點D的坐標為(6,m). 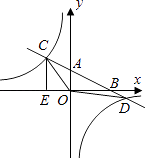
(1)求直線AB和反比例函數的解析式;
(2)求△OCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對x,y定義一種新運算x[]y= ![]() (其中a,b均為非零常數),這里等式右邊是通常的四則混合運算,例如:0[]2=
(其中a,b均為非零常數),這里等式右邊是通常的四則混合運算,例如:0[]2= ![]() =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.請解答下列問題.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),則稱M是m的函數,當自變量m在﹣1≤m≤3的范圍內取值時,函數值M為整數的個數記為k,求k的值;
(2)若x[]y=y[]x,對任意實數x,y都成立(這里x[]y和y[]x均有意義),求a與b的函數關系式?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c,自變量x與函數y的對應值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列說法正確的是( )
A.拋物線的開口向下
B.當x>﹣3時,y隨x的增大而增大
C.二次函數的最小值是﹣2
D.拋物線的對稱軸是x=﹣ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸交于點A(﹣1,0),頂點坐標為(1,n),與y軸的交點在(0,2)、(0,3)之間(包含端點).有下列結論: ①當x=3時,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ![]() ;
;
④ ![]() ≤n≤4.
≤n≤4.
其中正確的有( )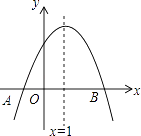
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、C、N三點在同一直線上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,則∠BCM:∠BCN=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一天,某客運公司的甲、乙兩輛客車分別從相距380千米的A、B兩地同時出發相向而行,并以各自的速度勻速行駛,兩車行駛2小時時甲車先到達服務區C地,此時兩車相距20千米,甲車在服務區C地休息了20分鐘,然后按原速度開往B地;乙車行駛2小時15分鐘時也經過C地,未停留繼續開往A地.(友情提醒:畫出線段圖幫助分析)
(1)乙車的速度是________千米/小時,B、C兩地的距離是________千米, A、C兩地的距離是________千米;
(2)求甲車的速度;
(3)這一天,乙車出發多長時間,兩車相距200千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知三條互相平行的直線a、b、c,請問能否作出一個等邊△ABC,使其三個頂點A、B、C分別在直線a、b、c上?(用“能”或“不能”填空).若能,請說明作圖方法;若不能,請簡要說明理由. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y=(3-2m)x+m-1是y關于x的一次函數.
(1)若y隨著x的增大而減小,求m的取值范圍;
(2)若函數的圖象與直線y=-3x平行,試確定該函數的表達式;
(3)若函數的圖象經過點(-1,5m+2),試確定該函數的表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com