
【題目】已知等腰三角形△ABC,BC邊上的高恰好等于BC邊長的一半,則∠BAC的度數是( )
A.75°B.90°或75°C.90°或 75°或15°D.75°或15°或60°
【答案】C
【解析】
本題要分情況討論,根據等腰三角形的性質來①當AD在三角形的內部,②AD在三角形的外部以,③BC邊為等腰三角形的底邊三種情況.
分三種情況:①AB=BC,AD⊥BC,AD在三角形的內部,
由題意知,AD=![]() BC=
BC=![]() AB,
AB,
∵∠ADB=90°,
∴∠B=30°,∠C=![]() =75°,
=75°,
∴∠BAC=∠C=75°;

②AC=BC,AD⊥BC,AD在三角形的外部,
由題意知,AD=![]() BC=
BC=![]() AC,
AC,
∵∠ADB=90°,
∴∠ACD=30°=∠B+∠CAB,
∵∠B=∠CAB,
∴∠BAC=15°;
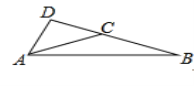
③AC=AB,AD⊥BC,BC邊為等腰三角形的底邊,
由等腰三角形的三線合一知點D為BC的中點,
由題意知,AD=![]() BC=CD=BD,
BC=CD=BD,
∴△ABD,△ADC均為等腰直角三角形,
∴∠BAD=∠CAD=45°,
∴∠BAC=90°,

∴∠BAC的度數為90°或75°或15°,
故選:C.


科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,AB=AC,D、E是斜邊BC上兩點,且∠DAE=45°,將△ADC繞點A順時針旋轉90°后,得到△AFB,連接EF,下列結論①△AEF≌△AED;②∠AED=45°;③BE+DC=DE; ④BE![]() +DC
+DC![]() =DE
=DE![]() ,其中正確的是( )
,其中正確的是( )

A. ②④ B. ①④ C. ②③ D. ①③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
關于x的方程:x+![]() =c+
=c+![]() 的解為x1=c,x2=
的解為x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可變形為x+
(可變形為x+![]() =c+
=c+![]() )的解為x1=c,x2=
)的解為x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解為x1=c,x2=
的解為x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解為x1=c,x2=
的解為x1=c,x2=![]() Z.
Z.
(1)歸納結論:根據上述方程與解的特征,得到關于x的方程x+![]() =c+
=c+![]() (m≠0)的解為 .
(m≠0)的解為 .
(2)應用結論:解關于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設x1、x2是一元二次方程2x2﹣7x+5=0的兩根,利用一元二次方程根與系數的關系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班級同學從學校出發去太陽島研學旅行,一部分乘坐大客車先出發,余下的同學20min后乘坐小轎車沿同一路線出行,大客車中途停車等候5min,小轎車趕上來之后,大客車以出發時速度的![]() 繼續行駛,小轎車保持原速度不變.小轎車司機因路線不熟錯過了景點入口,在駛過景點入口6 km時,原路提速返回,恰好與大客車同時到達景點入口.兩車距學校的路程S(單位:km)和行駛時間t(單位:min)之間的函數關系如圖所示.
繼續行駛,小轎車保持原速度不變.小轎車司機因路線不熟錯過了景點入口,在駛過景點入口6 km時,原路提速返回,恰好與大客車同時到達景點入口.兩車距學校的路程S(單位:km)和行駛時間t(單位:min)之間的函數關系如圖所示.
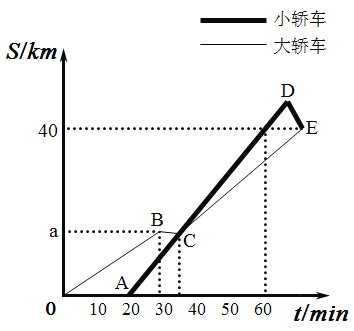
請結合圖象解決下面問題:
(1)學校到景點的路程為________km,![]() ________;
________;
(2)在小轎車司機駛過景點入口時,大客車離景點入口還有多遠?
(3)小轎車司機到達景點入口時發現本路段限速80 km/h,請你幫助小轎車司機計算折返時是否超速?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區教研部門對本區初二年級的學生進行了一次隨機抽樣問卷調查,其中有這樣一個問題:老師在課堂上放手讓學生提問和表達( )
A.從不 B.很少 C.有時 D.常常 E.總是
答題的學生在這五個選項中只能選擇一項.下面是根據學生對該問題的答卷情況繪制的兩幅不完整的統計圖.
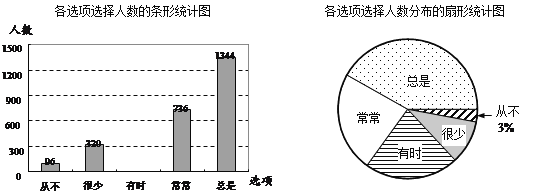
根據以上信息,解答下列問題:
(1)該區共有 名初二年級的學生參加了本次問卷調查;
(2)請把這幅條形統計圖補充完整;
(3)在扇形統計圖中,“總是”的圓心角為 .(精確到度)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某射擊運動員練習射擊,![]() 次成績分別是:
次成績分別是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (單位:環).下列說法中正確的是( )
(單位:環).下列說法中正確的是( )
A. 若這![]() 次成績的中位數為
次成績的中位數為![]() ,則
,則![]() B. 若這
B. 若這![]() 次成績的眾數是
次成績的眾數是![]() ,則
,則![]()
C. 若這![]() 次成績的方差為
次成績的方差為![]() ,則
,則![]() D. 若這
D. 若這![]() 次成績的平均成績是
次成績的平均成績是![]() ,則
,則![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提高產品的附加值,某公司計劃將研發生產的1200件新產品進行精加工后再投放市場.現有甲、乙兩個工廠都具備加工能力,公司派出相關人員分別到這兩個工廠了解情況,獲得如下信息:
信息一:甲工廠單獨加工完成這批產品比乙工廠單獨加工完成這批產品多用10天;
信息二:乙工廠每天加工的數量是甲工廠每天加工數量的1.5倍.
根據以上信息,求甲、乙兩個工廠每天分別能加工多少件新產品.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com