
【題目】把一副三角板按如圖放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜邊AC=BD=10,若將三角板DEB繞點B逆時針旋轉45°得到△D′E′B,則點A在△D′E′B的( ) 
A.內部
B.外部
C.邊上
D.以上都有可能
【答案】C
【解析】解:∵AC=BD=10,
又∵∠ABC=∠DEB=90°,∠A=45°,∠D=30°,
∴BE=5,AB=BC=5 ![]() ,
,
由三角板DEB繞點B逆時針旋轉45°得到△D′E′B,設△D′E′B與直線AB交于G,可知:∠EBE′=45°,∠E′=∠DEB=90°,
∴△GE′B是等腰直角三角形,且BE′=BE=5,
∴BG= ![]() =5
=5 ![]() ,
,
∴BG=AB,
∴點A在△D′E′B的邊上,
故選C.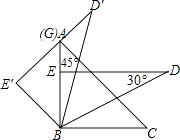
先根據勾股定理求出兩直角三角形的各邊長,再由旋轉的性質得:∠EBE′=45°,∠E′=∠DEB=90°,求出E′D′與直線AB的交點到B的距離也是5 ![]() ,與AB的值相等,所以點A在△D′E′B的邊上.本題考查了旋轉的性質和勾股定理,利用30°和45°的直角三角形的性質求出各邊的長;注意:在直角三角形中,30度角所對的直角邊等于斜邊的一半,45°角所對的兩直角邊相等,熟練掌握此內容是解決問題的關鍵.
,與AB的值相等,所以點A在△D′E′B的邊上.本題考查了旋轉的性質和勾股定理,利用30°和45°的直角三角形的性質求出各邊的長;注意:在直角三角形中,30度角所對的直角邊等于斜邊的一半,45°角所對的兩直角邊相等,熟練掌握此內容是解決問題的關鍵.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:初中數學 來源: 題型:
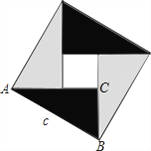
【題目】中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若![]() ,請你利用這個圖形解決下列問題:
,請你利用這個圖形解決下列問題:
(1)試說明![]() ;
;
(2)如果大正方形的面積是10,小正方形的面積是2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
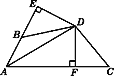
【題目】如圖,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求證:AD平分∠BAC;
(2)猜想寫出AB+AC與AE之間的數量關系并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解該校九年級學生2016年適應性考試數學成績,現從九年級學生中隨機抽取部分學生的適應性考試數學成績,按A,B,C,D四個等級進行統計,并將統計結果繪制成如圖所示不完整的統計圖,請根據統計圖中的信息解答下列問題:
(說明:A等級:135分﹣150分 B等級:120分﹣135分,C等級:90分﹣120分,D等級:0分﹣90分)
(1)此次抽查的學生人數為;
(2)把條形統計圖和扇形統計圖補充完整;
(3)若該校九年級有學生1200人,請估計在這次適應性考試中數學成績達到120分(包含120分)以上的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的外接圓,AB是⊙O的直徑,AB=8. 
(1)利用尺規,作∠CAB的平分線,交⊙O于點D;(保留作圖痕跡,不寫作法)
(2)在(1)的條件下,連接CD,OD,若AC=CD,求∠B的度數;
(3)在(2)的條件下,OD交BC于點E,求由線段ED,BE, ![]() 所圍成區域的面積.(其中
所圍成區域的面積.(其中 ![]() 表示劣弧,結果保留π和根號)
表示劣弧,結果保留π和根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C、D在圓上,且四邊形AOCD是平行四邊形,過點D作⊙O的切線,分別交OA延長線與OC延長線于點E、F,連接BF. 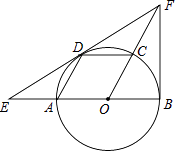
(1)求證:BF是⊙O的切線;
(2)已知圓的半徑為1,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“立德樹人,志愿服務”活動月中,學校團委為了解本校學生一個月內參加志愿服務次數的情況,隨機抽取了部分同學進行統計,并將統計結果分別分成A、B、C、D四類,根據統計結果繪制了如圖所示的兩幅不完整的統計圖.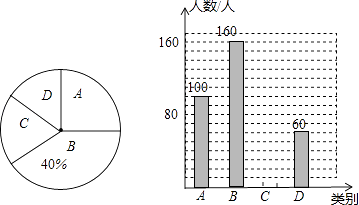
請根據圖中信息解答下列問題:
(1)本次抽樣調查了名學生,并請補全條形統計圖;
(2)被調查學生“一個月內參加志愿服務次數”的人數的眾數落在類.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠ABC、∠ACB的平分線BD,CE相交于O點,且BD交AC于點D,CE交AB于點E.某同學分析圖形后得出以下結論:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述結論一定正確的是
BCE;上述結論一定正確的是

A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com