
【題目】在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于A、B(A點在B點的左側)與
軸交于A、B(A點在B點的左側)與![]() 軸交于點C.
軸交于點C.
(1)如圖1,連接AC、BC,若△ABC的面積為3時,求拋物線的解析式;
(2)如圖2,點P為第四象限拋物線上一點,連接PC,若![]() 時,求點P的橫坐標;
時,求點P的橫坐標;
(3)如圖3,在(2)的條件下,點F在AP上,過點P作PH⊥![]() 軸于H點,點K在PH的延長線上,AK=KF,∠KAH=∠FKH,PF=
軸于H點,點K在PH的延長線上,AK=KF,∠KAH=∠FKH,PF=![]() ,連接KB并延長交拋物線于點Q,求PQ的長.
,連接KB并延長交拋物線于點Q,求PQ的長.

【答案】(1)解析式為![]() ;(2)點P 的橫坐標為6 ;
;(2)點P 的橫坐標為6 ;
(3) QP=7
【解析】試題分析:(1)通過解方程ax2-5ax+4a=0可得到A(1,0),B(4,0),然后利用三角形面積公式求出OC得到C點坐標,再把C點坐標代入y=ax2-5ax+4a中求出a即可得到拋物線的解析式;
(2)過點P作PH⊥x軸于H,作CD⊥PH于點H,如圖2,設P(x,ax2-5ax+4a),則PD=-ax2+5ax,通過證明Rt△PCD∽Rt△CBO,利用相似比可得到(-ax2+5ax):(-4a)=x:4,然后解方程求出x即可得到點P的橫坐標;
(3)過點F作FG⊥PK于點G,如圖3,先證明∠HAP=∠KPA得到HA=HP,由于P(6,10a),則可得到-10a=6-1,解得a=-![]() ,再判斷Rt△PFG單位等腰直角三角形得到FG=PG=
,再判斷Rt△PFG單位等腰直角三角形得到FG=PG=![]() PF=2,接著證明△AKH≌△KFG,得到KH=FG=2,則K(6,2),然后利用待定系數法求出直線KB的解析式為y=x-4,再通過解方程組
PF=2,接著證明△AKH≌△KFG,得到KH=FG=2,則K(6,2),然后利用待定系數法求出直線KB的解析式為y=x-4,再通過解方程組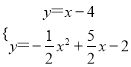 得到Q(-1,-5),利用P、Q點的坐標可判斷PQ∥x軸,于是可得到QP=7.
得到Q(-1,-5),利用P、Q點的坐標可判斷PQ∥x軸,于是可得到QP=7.
試題解析:(1)當y=0時,ax2-5ax+4a=0,解得x1=1,x2=4,則A(1,0),B(4,0),
∴AB=3,
∵△ABC的面積為3,
∴![]() ,解得OC=2,則C(0,-2),
,解得OC=2,則C(0,-2),
把C(0,-2)代入y=ax2-5ax+4a得4a=-2,解得a=-![]() ,
,
∴拋物線的解析式為y=-![]() x2+
x2+![]() x-2;
x-2;
(2)過點P作PH⊥x軸于H,作CD⊥PH于點H,如圖2,設P(x,ax2-5ax+4a),則PD=4a-(ax2-5ax+4a)=-ax2+5ax,
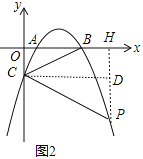
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BCP=2∠ABC,
∴∠PCD=∠ABC,
∴Rt△PCD∽Rt△CO,
∴PD:OC=CD:OB,
即(-ax2+5ax):(-4a)=x:4,解得x1=0,x2=6,
∴點P的橫坐標為6;
(3)過點F作FG⊥PK于點G,如圖3,
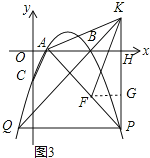
∵AK=FK,
∴∠KAF=∠KFA,
而∠KAF=∠KAH+∠PAH,∠KFA=∠PKF+∠KPF,
∵∠KAH=∠FKP,
∴∠HAP=∠KPA,
∴HA=HP,
∴△AHP為等腰直角三角形,
∵P(6,10a),
∴-10a=6-1,解得a=-![]() ,
,
在Rt△PFG中,∵PF=4![]() a=2
a=2![]() ,∠FPG=45°,
,∠FPG=45°,
∴FG=PG=![]() PF=2,
PF=2,
在△AKH和△KFG中
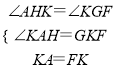 ,
,
∴△AKH≌△KFG,
∴KH=FG=2,
∴K(6,2),
設直線KB的解析式為y=mx+n,
把K(6,2),B(4,0)代入得
![]() ,
,
解得![]() ,
,
∴直線KB的解析式為y=x-4,
當a=-![]() 時,拋物線的解析式為y=-
時,拋物線的解析式為y=-![]() x2+
x2+![]() x-2,
x-2,
解方程組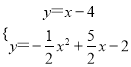 ,
,
解得![]() 或
或![]() ,
,
∴Q(-1,-5),
而P(6,-5),
∴PQ∥x軸,
∴QP=7.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結論: ①DG=DF; ②四邊形EFDG是菱形; ③![]() ;
;
④當![]() 時,BE的長為
時,BE的長為![]() ,其中正確的結論個數是( )
,其中正確的結論個數是( )
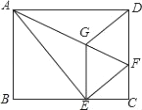
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查中適合用抽樣調查的方式來收集數據的有( )
①調查某型號平板電腦的使用壽命;②調查你所在班級中是否有同一天過生日的同學;③調查某種炮彈的殺傷半徑;④調查全國九年級學生完成課后作業所用的時間;⑤調查某種食品添加劑使用的情況;⑥調查你所在學校教師的健康情況.
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,BC∥OA,∠B=∠A=100°,試回答下列問題: 
(1)如圖①,求證:OB∥AC.
(2)如圖②,若點E、F在線段BC上,且滿足∠FOC=∠AOC,并且OE平分∠BOF.則∠EOC的度數等于;(在橫線上填上答案即可).
(3)在(2)的條件下,若平行移動AC,如圖③,那么∠OCB:∠OFB的值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值.
(4)在(3)的條件下,如果平行移動AC的過程中,若使∠OEB=∠OCA,此時∠OCA度數等于 . (在橫線上填上答案即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數y=![]() (x>0)的圖象與BC邊交于點E.
(x>0)的圖象與BC邊交于點E.
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積最大,最大面積是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com