
【題目】如圖,△ABC中,AD⊥BC,CE⊥AB,垂足分別為D、E,AD、CE交于點H,請你添加一個適當的條件: , 使△AEH≌△CEB.
【答案】AH=CB或EH=EB或AE=CE
【解析】解:∵AD⊥BC,CE⊥AB,垂足分別為D、E,
∴∠BEC=∠AEC=90°,
在Rt△AEH中,∠EAH=90°﹣∠AHE,
又∵∠EAH=∠BAD,
∴∠BAD=90°﹣∠AHE,
在Rt△AEH和Rt△CDH中,∠CHD=∠AHE,
∴∠EAH=∠DCH,
∴∠EAH=90°﹣∠CHD=∠BCE,
所以根據AAS添加AH=CB或EH=EB;
根據ASA添加AE=CE.
可證△AEH≌△CEB.
故填空答案:AH=CB或EH=EB或AE=CE.
開放型題型,根據垂直關系,可以判斷△AEH與△CEB有兩對對應角相等,就只需要找它們的一對對應邊相等就可以了.本題考查三角形全等的判定方法;判定兩個三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加時注意:AAA、SSA不能判定兩個三角形全等,不能添加,根據已知結合圖形及判定方法選擇條件是正確解答本題的關鍵.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,∠ACB=90°,點D、E在AB上,將△ACD、△BCE分別沿CD、CE翻折,點A、B分別落在點A′、B′的位置,再將△A′CD、△B′CE分別沿A′C、B′C翻折,點D與點E恰好重合于點O,則∠A′OB′的度數是( )

A.90° B.120° C.135° D.150°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 甲、乙兩名車工都加工要求尺寸是直徑10毫米的零件.從他們所生產的零件中,各取5件,測得直徑如下(單位:毫米)
甲:10.05, 10.02,9.97,9.95,10.01
乙:9.99,10.02,10.02,9.98,10.01
分別計算兩組數據的標準差(精確到0.01),說明在尺寸符合規格方面,誰做得較好?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次籃球聯賽初賽階段,每隊有![]() 場比賽,每場比賽都要分出勝負,每隊勝一場得
場比賽,每場比賽都要分出勝負,每隊勝一場得![]() 分, 負一場得
分, 負一場得![]() 分,積分超過
分,積分超過![]() 分才能獲得參賽資格.
分才能獲得參賽資格.
(1)已知甲隊在初賽階段的積分為![]() 分,求甲隊初賽階段勝、負各多少場;
分,求甲隊初賽階段勝、負各多少場;
(2)如果乙隊要獲得參加決賽資格,那么乙隊在初賽階段至少要勝多少場?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,2,3分別以△ABC的AB和AC為邊向△ABC外作正三角形(等邊三角形)、正四邊形(正方形)、正五邊形,BE和CD相交于點O.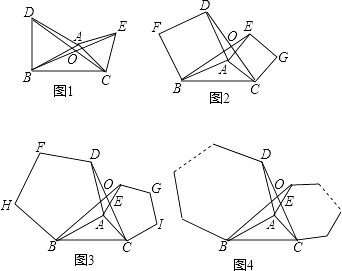
(1)在圖1中,求證:△ABE≌△ADC.
(2)由(1)證得△ABE≌△ADC,由此可推得在圖1中∠BOC=120°,請你探索在圖2中,∠BOC的度數,并說明理由或寫出證明過程.
(3)填空:在上述(1)(2)的基礎上可得在圖3中∠BOC=(填寫度數).
(4)由此推廣到一般情形(如圖4),分別以△ABC的AB和AC為邊向△ABC外作正n邊形,BE和CD仍相交于點O,猜想得∠BOC的度數為(用含n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備租用一批汽車,現有甲、乙兩種大客車,甲種客車每輛載客量45人,乙種客車每輛載客量30人,已知1輛甲種客車和3輛乙種客車共需租金1240元,3輛甲種客車和2輛乙種客車共需租金1760元.
(1)求1輛甲種客車和1輛乙種客車的租金分別是多少元?
(2)學校計劃租用甲、乙兩種客車共8輛,送330名師生集體外出活動,最節省的租車費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)(問題引領)
問題1:在四邊形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分別是AB,AD上的點.且∠ECF=60°.探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是,延長FD到點G.使DG=BE.連結CG,先證明
△CBE≌△CDG,再證明△CEF≌△CGF.他得出的正確結論是________________.

(探究思考)
問題2:若將問題1的條件改為:四邊形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 問題1的結論是否仍然成立?請說明理由.
∠BCD, 問題1的結論是否仍然成立?請說明理由.

(拓展延伸)
問題3:在問題2的條件下,若點E在AB的延長線上,點F在DA的延長線上,則問題2的結論是否仍然成立?若不成立,猜測此時線段BE、DF、EF之間存在什么樣的等量關系?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某教育局為了解七年級學生一個學期參加綜合實踐活動的情況,隨機抽樣調查了某校七年級學生一個學期參加綜合實踐活動的天數,并用得到的數據繪制了下面兩幅不完整的統計圖(如圖),請你根據圖中提供的信息,回答下列問題:
(1)求出該校七年級學生總數;
(2)在這次抽樣調查中,眾數和中位數分別是多少?


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com