Question

【題目】如圖1，拋物線y=ax2+bx+ 經過A（1，0），B（7，0）兩點，交y軸于D點，以AB為邊在x軸上方作等邊三角形ABC．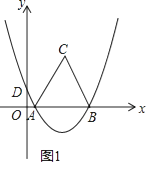

（1）求拋物線的解析式；
（2）在x軸上方的拋物線上是否存在點M，是S△ABM= S△ABC？若存在，請求出點M的坐標；若不存在，請說明理由；
（3）如圖2，E是線段AC上的動點，F是線段BC上的動點，AF與BE相交于點P．
①若CE=BF，試猜想AF與BE的數量關系及∠APB的度數，并說明理由；
②若AF=BE，當點E由A運動到C時，請直接寫出點P經過的路徑長．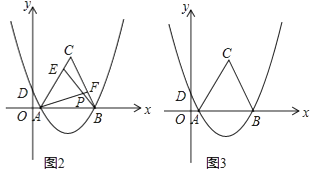

Answer 1

【答案】
（1）解：將點A（1，0），B（7，0）代入拋物線的解析式得： ，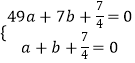

解得：a= ，b=﹣2．

∴拋物線的解析式為y= x2﹣2x+ ．

（2）解：存在點M，使得S△ABM= S△ABC．

理由：如圖所示：過點C作CK⊥x軸，垂足為K．

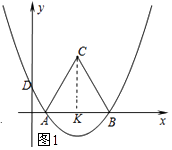
∵△ABC為等邊三角形，

∴AB=BC=AC=6，∠ACB=60°．

∵CK⊥AB，

∴KA=BK=3，∠ACK=30°．

∴CK=3 ．

∴S△ABC= ABCK= ×6×3=9 ．

∴S△ABM= ×9 =12．

設M（a， a2﹣2a+ ）．

∴ AB|y|=12，即 ×6×（ a2﹣2a+ ）=12，

解得：a1=9，a2=﹣1．

∴點M的坐標為（9，4）或（﹣1，4）．

（3）解：①結論：AF=BE，∠APB=120°．

∵△ABC為等邊三角形，

∴BC=AB，∠C=∠ABF．

∵在△BEC和△AFB中 ，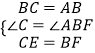

∴△BEC≌△AFB．

∴AF=BE，∠CBE=∠BAF．

∴∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°．

∴∠APB=180°﹣60°=120°．

②當AE≠BF時，由①可知點P在以AB為直徑的圓上，過點M作ME⊥AB，垂足為E．

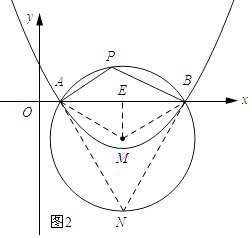
∵∠APB=120°，

∴∠N=60°．

∴∠AMB=120°．

又∵ME⊥AB，垂足為E，

∴AE=BE=3，∠AME=60°．

∴AM=2 ．

∴點P運動的路徑= = ．

當AE=BF時，點P在AB的垂直平分線上時，如圖所示：過點C作CK⊥AB，則點P運動的路徑=CK的長．

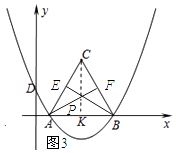
∵AC=6，∠CAK=60°，

∴KC=3 ．

∴點P運動的路徑為3 ．

綜上所述，點P運動的路徑為3 或 ．

【解析】（1）將點A、B兩點坐標代入函數解析式，建立方程組，即可求出拋物線的解析式。
（2）已知△ABC為等邊三角形，要求此三角形的面積，添加輔助線，過點C作CK⊥x軸，求出△ABC的高CK的長，就可以求出△ABC的面積；根據S△ABM 和S△ABC的關系，求出S△ABM的值，由點M在x軸上方的拋物線上，設出點M的坐標，根據S△ABM=12，建立方程，即可求出點M的坐標。
（3）①根據已知，易證得△BEC≌△AFB．可得AF=BE，∠CBE=∠BAF．再求出∠FAB+∠ABP的度數，即可求得∠APB度數；②分兩種情況：當AE≠BF時，由①可知點P在以AB為直徑的圓上，過點M作ME⊥AB，垂足為E．根據圓內接四邊形的對角互補，求出∠N的度數，根據圓周角定理，求出∠AMB的度數，然后過點E作ME⊥AB，垂足為E，就可以求出AM的長，即可求出點P的運動路徑長；當AE=BF時，點P在AB的垂直平分線上時，如圖所示：過點C作CK⊥AB，則點P運動的路徑=CK的長，在Rt△AKC中，易求出KC的長。
【考點精析】關于本題考查的解直角三角形，需要了解解直角三角形的依據：①邊的關系a2+b2=c2；②角的關系：A+B=90°；③邊角關系：三角函數的定義．(注意：盡量避免使用中間數據和除法)才能得出正確答案．