
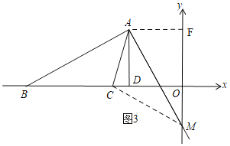
【題目】在平面直角坐標系中,點A的坐標為(﹣6,6),以A為頂點的∠BAC的兩邊始終與x軸交于B、C兩點(B在C左面),且∠BAC=45°.
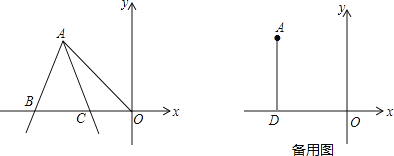
(1)如圖,連接OA,當AB=AC時,試說明:OA=OB.
(2)過點A作AD⊥x軸,垂足為D,當DC=2時,將∠BAC沿AC所在直線翻折,翻折后邊AB交y軸于點M,求點M的坐標.
【答案】(1)見解析;(2) M的坐標為(0,3)或(0,-6)
【解析】
(1)利用等腰三角形的性質求得∠BAO和∠ABC的度數,然后利用等角對等邊即可證得;
(2)當點C在點D右側時,連接CM,過點A作AE⊥y軸于點E,證明△BAD≌△MAE,在Rt△COM中,由勾股定理即可求得M的坐標;當點C在點D左側時,連接CM,過點A作AF⊥y軸于點F,證明△BAD≌△MAF,同理,在Rt△COM中,由勾股定理即可求得M的坐標.
(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
過點A作AE⊥OB于E,
∵A(-6,6),
∴△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=![]() ∠BAC=22.5°.
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)設OM=x,
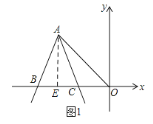
當點C在點D右側時,如圖2,連接CM,過點A作AE⊥y軸于點E,
由∠BAM=∠DAE=90°,
可知:∠BAD=∠MAE;
∴在△BAD和△MAE中,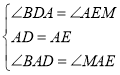 ,
,
∴△BAD≌△MAE.
∴BD=EM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M點坐標為(0,3).
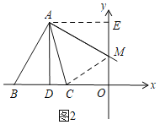
當點C在點D左側時,如圖3,連接CM,過點A作AF⊥y軸于點F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M點坐標為(0,-6).
綜上,M的坐標為(0,3)或(0,-6).


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形 ABCD,點 E,F 分別在 AD,CD 上,且DE=CF,AF 與 BE 相交于點G.
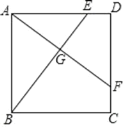
(1)求證:AF⊥BE;
(2)若 AB=6,DE=2,AG的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,以
,以![]() 邊
邊![]() 和
和![]() 為邊作等邊
為邊作等邊![]() 和
和![]() ,連接
,連接![]() ,
,![]() ,
,
![]() 判斷
判斷![]() 與
與![]() 的數量關系,并求
的數量關系,并求![]() 與
與![]() 的夾角
的夾角![]() 的度數;
的度數;
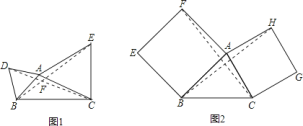
![]() 繼續探索,如圖
繼續探索,如圖![]() ,以
,以![]() 的
的![]() 和
和![]() 為邊作正方形
為邊作正方形![]() 和
和![]() ,連接
,連接![]() 、
、![]() ,判斷
,判斷![]() 和
和![]() 的數量關系,并求出此時
的數量關系,并求出此時![]() 與
與![]() 的夾角;
的夾角;
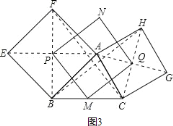
![]() 如圖
如圖![]() 中
中![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 、
、![]() 分別是正方形的中心,順次連接
分別是正方形的中心,順次連接![]() ,判斷四邊形
,判斷四邊形![]() 的形狀并證明.
的形狀并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于二次函數![]() 的圖象與性質,下列結論錯誤的是 ( )
的圖象與性質,下列結論錯誤的是 ( )
A. 當x=3時,函數有最大值-2
B. 當x>3時,y隨x的增大而減小
C. 拋物線可由 ![]() 經過平移得到
經過平移得到
D. 該函數的圖象與x軸有兩個交點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年,在端午節前夕,三位同學到某超市調研一種進價為2元的粽子的銷售情況.(售價不低于進價).請根據小麗提供的信息,解答小華和小明提出的問題.

認真閱讀上面三位同學的對話,請根據小麗提供的信息.
(1)解答小華的問題;
(2)解答小明的問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a>0)的對稱軸為直線x=-1,與x軸的一個交點為(x1,0),且0<x1<1,下列結論:①9a-3b+c>0;②b<c;③3a+c>0,其中正確結論兩個數有______。
查看答案和解析>>
科目:初中數學 來源: 題型:
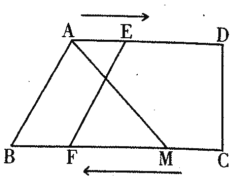
【題目】如圖,四邊形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一點,且BM=9cm,點E從點A出發以1cm/s的速度向點D運動,點F從點C出發,以3cm/s的速度向點B運動,當其中一點到達終點,另一點也隨之停止,設運動時間為t,則當以A、M、E、F為頂點的四邊形是平行四邊形時,t=__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com