
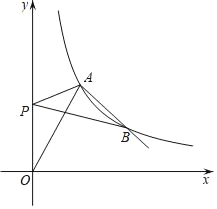
【題目】如圖,函數y=![]() 的圖象與雙曲線y=
的圖象與雙曲線y=![]() (k≠0,x>0)相交于點A(3,m)和點B.
(k≠0,x>0)相交于點A(3,m)和點B.
(1)求雙曲線的解析式及點B的坐標;
(2)若點P在y軸上,連接PA,PB,求當PA+PB的值最小時點P的坐標.
【答案】(1)雙曲線的解析式為y=![]() ,點B的坐標為(6,3);點P的坐標為(0,5).
,點B的坐標為(6,3);點P的坐標為(0,5).
【解析】分析:(1)由一次函數的解析式可得點A的坐標,從而求出反比例函數的解析式,解由一次函數與反比例函數的解析式組成的方程組可求點B的坐標;(2)作點A關于y軸的對稱點A′,連接A′B,直線A′B與y的交點即為點P,用待定系數法求直線A′B的解析式后即可求點P的坐標.
詳解:(1)把A(3,m)代入y=2x,可得m=2×3=6,∴A(3,6),
把A(3,6)代入y=![]() ,可得k=3×6=18,
,可得k=3×6=18,
∴雙曲線的解析式為y=![]() ;
;
當x>3時,解方程組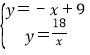 ,可得
,可得![]() 或
或![]() (舍去)
(舍去)
∴點B的坐標為(6,3).
(2)如圖所示,作點A關于y軸的對稱點A′(-3,6),連接A′P,則A′P=AP,
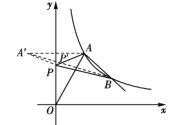
∴PA+PB=A′P+BP≥A′B
當A′,P,B三點共線時,PA+PB的最小值等于A′B的長.
設A′B的解析式為y=ax+b,
把A′(-3,6),B(6,3)代入,可得![]() ,解得
,解得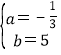 .
.
∴A′B的解析式為y=![]() x+5,
x+5,
令x=0,則y=5,
∴點P的坐標為(0,5).


 全能練考卷系列答案
全能練考卷系列答案科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并解答其后的問題:
我國古代南宋數學家秦九韶在其所著書《數學九章》中,利用“三斜求積術”十分巧妙的解決了已知三角形三邊求其面積的問題,這與西方著名的“海倫公式”是完全等價的.我們也稱這個公式為“海倫秦九韶公式”,該公式是:設△ABC中,∠A、∠B、∠C所對的邊分別為a、b、c,△ABC的面積為S=![]() .
.
(1)(舉例應用)已知△ABC中,∠A、∠B、∠C所對的邊分別為a、b、c,且a=4,b=5,c=7,則△ABC的面積為 ;
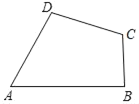
(2)(實際應用)有一塊四邊形的草地如圖所示,現測得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求該塊草地的面積.
m,∠A=60°,求該塊草地的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
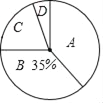
【題目】2017年4月15日至5月15日,某市約8萬名初三畢業生參加了中考體育測試,為了了解今年初三畢業生的體育成績,從某校隨機抽取了60名學生的測試成績,根據測試評分標準,將他們的得分按優秀、良好、及格、不及格(分別用A、B、C、D表示)四個等級進行統計,并繪制成下面的扇形圖和統計表:
等級 | 成績(分) | 頻數(人數) | 頻率 |
A | 27~30 | 24 | 0.4 |
B | 23~26 | m | x |
C | 19~22 | n | y |
D | 18及18以下 | 3 | 0.05 |
合計 | 60 | 1.00 |
請你根據以上圖表提供的信息,解答下列問題:
(1)m= ,n= ,x= ,y= ;
(2)在扇形圖中,B等級所對應的圓心角是 度;
(3)請你估計某市這8萬名初三畢業生成績等級達到優秀和良好的大約有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成績均為A,現決定從這四名同學中選兩名參加學校組織的體育活動,直接寫出恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷一種雙肩包,已知這種雙肩包的成本價為每個30元.市場調查發現,這種雙肩包每天的銷售量y(單位:個)與銷售單價x(單位:元)有如下關系:y=-x+60(30≤x≤60).
設這種雙肩包每天的銷售利潤為w元.
(1)求w與x之間的函數解析式;
(2)這種雙肩包銷售單價定為多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果物價部門規定這種雙肩包的銷售單價不高于48元,該商店銷售這種雙肩包每天要獲得200元的銷售利潤,銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車從A城出發勻速行駛至B城,在整個行駛過程中,甲、乙兩車離開A城的距離y(km)與行駛的時間t(h)之間的函數關系如圖所示.
(1)求乙車離開A城的距離y關于t的函數解析式;
(2)求乙車的速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在家中利用物理知識稱量某個品牌純牛奶的凈含量,稱得六盒純牛奶的含量分別為:248mL,250mL,249mL,251mL,249mL,253mL,對于這組數據,下列說法正確的是( ).
A.平均數為251mL B.中位數為249mL
C.眾數為250mL D.方差為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級甲、乙兩班舉行電腦漢字輸入比賽,兩個班能參加比賽的學生每分鐘輸入漢字的個數,經統計和計算后結果如下表:

有一位同學根據上面表格得出如下結論:
①甲、乙兩班學生的平均水平相同;②乙班優秀人數比甲班優秀人數多(每分鐘輸入漢字達150個以上為優秀);③甲班學生比賽成績的波動比乙班學生比賽成績的波動大.
上述結論正確的是_______(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△ADF和△BCE中,∠A=∠B,點D,E,F,C在同一直線上,有如下三個關系式:①.AD=BC;②.DE=CF;③.BE∥AF.
⑴.請用其中兩個關系式作為條件,另一個作為結論,寫出所有正確的結論.
⑵.選擇(1)中你寫出的一個正確結論,說明它正確的理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P、Q是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s,連接AQ、CP交于點M,則在P、Q運動的過程中,下列結論錯誤的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度數不變,始終等于60°
D.當第![]() 秒或第
秒或第![]() 秒時,△PBQ為直角三角形
秒時,△PBQ為直角三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com