
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點A、C的坐標分別為(-1,0),(0,-3),直線x=1為拋物線的對稱軸.點D為拋物線的頂點,直線BC與對稱軸相較于點E.
(1)求拋物線的解析式并直接寫出點D的坐標;
(2)點P為直線x=1右方拋物線上的一點(點P不與點B重合).記A、B、C、P四點所構成的四邊形面積為S,若S=![]() S△BCD,求點P的坐標;
S△BCD,求點P的坐標;
(3)點Q是線段BD上的動點,將△DEQ延邊EQ翻折得到△D′EQ,是否存在點Q使得△D′EQ與△BEQ的重疊部分圖形為直角三角形?若存在,請求出BQ的長,若不存在,請說明理由.
【答案】(1)y=x2-2x-3,頂點D的坐標為(1,-4);(2)P點坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)存在,
);(3)存在,![]() 或
或![]() 1或
1或![]() -
-![]() ,
,
【解析】
試題分析:(1)利用拋物線的對稱性得到B(3,0),則設交點式為y=a(x+1)(x-3),把C(0,-3)代入求出a即可得到拋物線解析式,然后把解析式配成頂點式即可得到D點坐標;
(2)設P(m,m2-2m-3),先確定直線BC的解析式y=x-3,再確定E(1,-2),則可根據三角形面積公式計算出S△BDC=S△BDE+S△CDE=3,然后分類討論:當點P在x軸上方時,即m>3,如圖1,利用S=S△PAB+S△CAB=![]() S△BCD得到2m2-4m=
S△BCD得到2m2-4m=![]() ;當點P在x軸下方時,即1<m<3,如圖2,連結OP,利用S=S△AOC+S△COP+S△POB=
;當點P在x軸下方時,即1<m<3,如圖2,連結OP,利用S=S△AOC+S△COP+S△POB=![]() S△BCD得到-
S△BCD得到-![]() m2+
m2+![]() m+6=
m+6=![]() ,再分別解關于m的一元二次方程求出m,從而得到P點坐標;
,再分別解關于m的一元二次方程求出m,從而得到P點坐標;
(3)存在.直線x=1交x軸于F,利用兩點間的距離公式計算出BD=2![]() ,分類討論:①如圖3,EQ⊥DB于Q,證明Rt△DEQ∽Rt△DBF,利用相似比可計算出DQ=
,分類討論:①如圖3,EQ⊥DB于Q,證明Rt△DEQ∽Rt△DBF,利用相似比可計算出DQ=![]() ,則BQ=BD-DQ=
,則BQ=BD-DQ=![]() ;②如圖4,ED′⊥BD于H,證明Rt△DEQ=H∽Rt△DBF,利用相似比計算出DH=
;②如圖4,ED′⊥BD于H,證明Rt△DEQ=H∽Rt△DBF,利用相似比計算出DH=![]() ,EH=
,EH=![]() ,在Rt△QHD′中,設QH=x,D′Q=DQ=DH-HQ=
,在Rt△QHD′中,設QH=x,D′Q=DQ=DH-HQ=![]() -x,D′H=D′E-EH=DE-EH=2-
-x,D′H=D′E-EH=DE-EH=2-![]() ,則利用勾股定理可得x2+(2-
,則利用勾股定理可得x2+(2-![]() )2=(
)2=(![]() -x)2,解得x=1-
-x)2,解得x=1-![]() ,于是BQ=BD-DH+HQ-
,于是BQ=BD-DH+HQ-![]() =
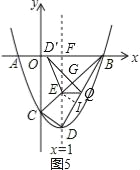
=![]() +1;③如圖5,D′Q⊥BC于G,作EI⊥BD于I,利用①得結論可得EI=
+1;③如圖5,D′Q⊥BC于G,作EI⊥BD于I,利用①得結論可得EI=![]() ,BI=
,BI=![]() ,而BE=2
,而BE=2![]() ,則BG=BE-EG=2
,則BG=BE-EG=2![]() -
-![]() ,根據折疊性質得∠EQD=∠EQD′,則根據角平分線性質得EG=EI=
,根據折疊性質得∠EQD=∠EQD′,則根據角平分線性質得EG=EI=![]() ,接著證明△BQG∽△BEI,利用相似比可得BQ=
,接著證明△BQG∽△BEI,利用相似比可得BQ=![]() -
-![]() ,所以當BQ為
,所以當BQ為![]() 或
或![]() +1或
+1或![]() -
-![]() 時,將△DEQ沿邊EQ翻折得到△D′EQ,使得△D′EQ與△BEQ的重疊部分圖形為直角三角形.
時,將△DEQ沿邊EQ翻折得到△D′EQ,使得△D′EQ與△BEQ的重疊部分圖形為直角三角形.
試題解析:(1)∵點A與點B關于直線x=1對稱,
∴B(3,0),
設拋物線解析式為y=a(x+1)(x-3),
把C(0,-3)代入得-3a=-3,解得a=1,
∴拋物線就笑著說為y=(x+1)(x-3)=x2-2x-3,
∵y=(x-1)2-4,
∴拋物線頂點D的坐標為(1,-4);
(2)設P(m,m2-2m-3),易得直線BC的解析式為y=x-3,
當x=1時,y=x-3=-3,則E(1,-2),
∴S△BDC=S△BDE+S△CDE=![]() ×3×(-2+4)=3,
×3×(-2+4)=3,
當點P在x軸上方時,即m>3,如圖1,
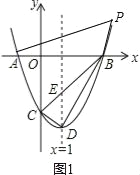
S=S△PAB+S△CAB=![]() 3(3+1)+
3(3+1)+![]() (3+1)(m2-2m-3)=2m2-4m,
(3+1)(m2-2m-3)=2m2-4m,
∵S=![]() S△BCD,
S△BCD,
∴2m2-4m=![]() ,
,
整理得4m2-8m-15=0,解得m1=![]() ,m2=
,m2=![]() (舍去),
(舍去),
∴P點坐標為(![]() ,
,![]() );
);
當點P在x軸下方時,即1<m<3,如圖2,連結OP,
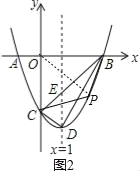
S=S△AOC+S△COP+S△POB=![]() 31+
31+![]() 3m+
3m+![]() 3(-m2+2m+3)=-
3(-m2+2m+3)=-![]() m2+
m2+![]() m+6,
m+6,
∵S=![]() S△BCD,
S△BCD,
∴-![]() m2+
m2+![]() m+6=
m+6=![]() ,
,
整理得m2-3m+1=0,解得m1=![]() ,m2=
,m2=![]() (舍去)
(舍去)
∴P點坐標為(![]() ,
,![]() ),
),
綜上所述,P點坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)存在.直線x=1交x軸于F,BD=![]() ,
,
①如圖3,EQ⊥DB于Q,△DEQ沿邊EQ翻折得到△D′EQ,

∵∠EDQ=∠BDF,
∴Rt△DEQ∽Rt△DBF,
∴![]() ,即
,即![]() ,解得DQ=
,解得DQ=![]() ,
,
∴BQ=BD-DQ=2![]() -
-![]() =
=![]() ;
;
②如圖4,ED′⊥BD于H,
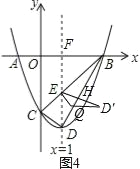
∵∠EDH=∠BDF,
∴Rt△DEQ=H∽Rt△DBF,
∴![]() ,即
,即![]() ,解得DH=
,解得DH=![]() ,EH=
,EH=![]() ,
,
在Rt△QHD′中,設QH=x,D′Q=DQ=DH-HQ=![]() -x,D′H=D′E-EH=DE-EH=2-
-x,D′H=D′E-EH=DE-EH=2-![]() ,
,
∴x2+(2-![]() )2=(
)2=(![]() -x)2,解得x=1-
-x)2,解得x=1-![]() ,
,
∴BQ=BD-DQ=BD-(DH-HQ)=BD-DH+HQ=2![]() -
-![]() +1-
+1-![]() =
=![]() +1;
+1;
③如圖5,D′Q⊥BC于G,作EI⊥BD于I,由①得EI=![]() ,BI=
,BI=![]() ,
,
∵BE=![]() ,
,
∴BG=BE-EG=2![]() -
-![]() ,
,
∵△DEQ沿邊EQ翻折得到△D′EQ,
∴∠EQD=∠EQD′,
∴EG=EI=![]() ,
,
∵∠GBQ=∠IBE,
∴△BQG∽△BEI,
∴![]() ,即
,即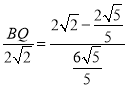
∴BQ=![]() -
-![]() ,
,
綜上所述,當BQ為![]() 或
或![]() 1或
1或![]() -
-![]() ,將△DEQ沿邊EQ翻折得到△D′EQ,使得△D′EQ與△BEQ的重疊部分圖形為直角三角形.
,將△DEQ沿邊EQ翻折得到△D′EQ,使得△D′EQ與△BEQ的重疊部分圖形為直角三角形.


科目:初中數學 來源: 題型:
【題目】(1)2(x2-2x+5)-3(2x2-5)=________________.
(2)4(m-3n)-5(3n-10m)-13(n-2m)=_________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個多項式加上5x2﹣4x﹣3得﹣x2﹣3x,則這個多項式為( )
A. 4x2﹣7x﹣3 B. 6x2﹣x﹣3 C. ﹣6x2+x+3 D. ﹣6x2﹣7x﹣3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】冰箱冷凍室的溫度為-6 ℃,此時房間內的溫度為20 ℃,則房間內的溫度比冰箱冷凍室的溫度高( )
A. 26 ℃ B. 14 ℃ C. -26 ℃ D. -14 ℃
查看答案和解析>>
科目:初中數學 來源: 題型:
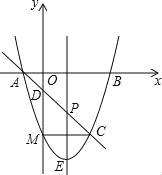
【題目】拋物線y=x2+bx+c與x軸交于點A(-1,0),B(3,0)兩點,過點A的直線交拋物線于點C(2,m),交y軸于點D.
(1)求拋物線及直線AC的解析式;
(2)點P是線段AC上的一動點(點P與點A、C不重合),過點P作y軸的平行線交拋物線于點E,求線段PE長度的最大值;
(3)點M(m,-3)是拋物線上一點,問在直線AC上是否存在點F,使△CMF是等腰直角三角形?如果存在,請求出點F的坐標;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com