
 如圖:△ABC中,AB=AC,內切圓⊙O與邊BC、AB分別切于點D、E、F,若∠C=30°,CE=2$\sqrt{3}$,則AC=4.
如圖:△ABC中,AB=AC,內切圓⊙O與邊BC、AB分別切于點D、E、F,若∠C=30°,CE=2$\sqrt{3}$,則AC=4. 分析 根據切線長定理,得到D是BC的中點,從而得到A,O,D三點共線.根據等腰三角形的三線合一得到直角三角形ACD.根據切線長定理得到CD=CE,則根據銳角三角函數即可求得AC的長.
解答 解: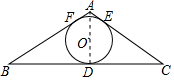 連接AO、OD;
連接AO、OD;
∵O是△ABC的內心,
∴OA平分∠BAC,
∵⊙O是△ABC的內切圓,D是切點,
∴OD⊥BC;
又∵AC=AB,
∴A、O、D三點共線,即AD⊥BC,
∵CD、CE是⊙O的切線,
∴CD=CE=2$\sqrt{3}$,
∵∠C=30°,CE=2$\sqrt{3}$,
∴CA=$\frac{CD}{cos∠C}$=4,
故答案為:4.
點評 本題運用了切線長定理和等腰三角形的三線合一的性質,關鍵是掌握等腰三角形的頂角平分線、底邊上的中線、底邊上的高相互重合.


科目:初中數學 來源: 題型:填空題
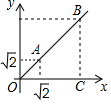 在平面直角坐標系中,點A($\sqrt{2}$,$\sqrt{2}$)、B(3$\sqrt{2}$,3$\sqrt{2}$ )動點C在x軸上,若以A、B、C三點為頂點的三角形是等腰三角形,則這樣的點C有3個.
在平面直角坐標系中,點A($\sqrt{2}$,$\sqrt{2}$)、B(3$\sqrt{2}$,3$\sqrt{2}$ )動點C在x軸上,若以A、B、C三點為頂點的三角形是等腰三角形,則這樣的點C有3個.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在矩形ABCD中,O為AC中點,EF過點O且EF⊥AC分別交DC于點F,交AB于點E,點G是AE中點且∠AOG=30°,給出以下結論:
如圖,在矩形ABCD中,O為AC中點,EF過點O且EF⊥AC分別交DC于點F,交AB于點E,點G是AE中點且∠AOG=30°,給出以下結論:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x3•x5=x15 | B. | (x2)5=x7 | C. | $\root{3}{27}$=3 | D. | $\frac{-a+b}{a+b}$=-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,⊙M與x軸相交于A(2,0)、B(8,0),與y軸相切于點C,P是優弧AB上的一點,則tan∠APB為( )
如圖,⊙M與x軸相交于A(2,0)、B(8,0),與y軸相切于點C,P是優弧AB上的一點,則tan∠APB為( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
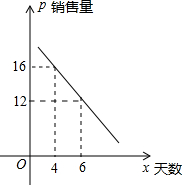 某水果店新進一種水果,進價為20元/盒,為了摸清行情,決定試營銷10天,商家通過這10天的市場調查發現:
某水果店新進一種水果,進價為20元/盒,為了摸清行情,決定試營銷10天,商家通過這10天的市場調查發現:| 天數 | 1≤x≤5 | 6≤x≤10 |
| 銷售價格y | $\frac{1}{2}$x+24 | 30 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
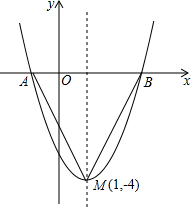 如圖:二次函數y=(x+m)2+k的圖象,其頂點坐標為M(1,-4).
如圖:二次函數y=(x+m)2+k的圖象,其頂點坐標為M(1,-4).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com