
【題目】某文具店準備購進A、B兩種品牌的文具袋進行銷售,若購進A品牌文具袋和B品牌文具袋各5個共花費120元,購進A品牌文具袋3個和B品牌文具袋4個共花費88元.
(1)求購進A品牌文具袋和B品牌文具袋的單價;
(2)若該文具店購進了A,B兩種品牌的文具袋共100個,其中A品牌文具袋售價為12元,B品牌文具袋售價為23元,設購進A品牌文具袋x個,獲得總利潤為w元.
①求w關于x的函數關系式;
②要使銷售文具袋的利潤最大,且所獲利潤不低于進貨價格的45%,請你幫該文具店設計一個進貨方案,并求出其所獲利潤的最大值.
【答案】(1)購進A品牌文具袋的單價為8元,B品牌文具袋的單價為16元;(2)①w=﹣3x+700;②購進A品牌文具袋34個,B品牌文具袋66個時,可以獲得最大利潤,最大利潤是598元.
【解析】
(1)根據購進![]() 品牌文具袋和
品牌文具袋和![]() 品牌文具袋各5個共花費120元,購進
品牌文具袋各5個共花費120元,購進![]() 品牌文具袋3個和
品牌文具袋3個和![]() 品牌文具袋4個共花費88元,可以列出相應的二元一次方程組,從而可以求得購進
品牌文具袋4個共花費88元,可以列出相應的二元一次方程組,從而可以求得購進![]() 品牌文具袋和
品牌文具袋和![]() 品牌文具袋的單價;
品牌文具袋的單價;
(2)①根據題意,可以寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
②根據所獲利潤不低于進貨價格的![]() ,可以得到
,可以得到![]() ,從而可以求得
,從而可以求得![]() 的取值范圍,然后根據一次函數的性質,即可解答本題.
的取值范圍,然后根據一次函數的性質,即可解答本題.
解:(1)設購進A品牌文具袋的單價為x元,B品牌文具袋的單價為y元,
由題意得:![]() ,得
,得![]() ,
,
答:購進A品牌文具袋的單價為8元,B品牌文具袋的單價為16元;
(2)①由題意可得,w=(12﹣8)x+(23﹣16)(100﹣x)=﹣3x+700,
即w關于x的函數關系式為w=﹣3x+700;
②∵所獲利潤不低于進貨價格的45%,
∴﹣3x+700≥[8x+16(100﹣x)]×45%,
解得:![]() ,
,
∵x為整數,w=﹣3x+700,
∴當x=34時,w取得最大值,此時w=598,100﹣x=66,
答:購進A品牌文具袋34個,B品牌文具袋66個時,可以獲得最大利潤,最大利潤是598元.


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+a與x軸交于點A(4,0),與y軸交于點B,拋物線y=
x+a與x軸交于點A(4,0),與y軸交于點B,拋物線y=![]() x2+bx+c經過點A,B.點M(m,0)為x軸上一動點,過點M且垂直于x軸的直線分別交直線AB及拋物線于點P,N.
x2+bx+c經過點A,B.點M(m,0)為x軸上一動點,過點M且垂直于x軸的直線分別交直線AB及拋物線于點P,N.
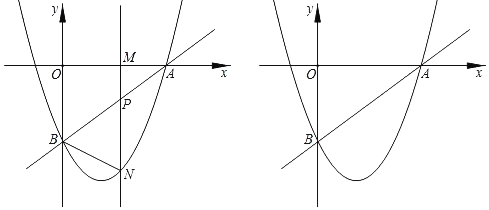
(1)填空:點B的坐標為 ,拋物線的解析式為 ;
(2)當點M在線段OA上運動時(不與點O,A重合),
①當m為何值時,線段PN最大值,并求出PN的最大值;②求出使△BPN為直角三角形時m的值;
(3)若拋物線上有且只有三個點N到直線AB的距離是h,請直接寫出此時由點O,B,N,P構成的四邊形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,點
,點![]() 在底邊
在底邊![]() 上,
上,![]() 的兩邊分別交
的兩邊分別交![]() 、
、![]() 所在直線于
所在直線于![]() 、
、![]() 兩點,
兩點,![]() ,
,![]() .
.
(1)如圖1,若![]() ,
,![]() ,求證:
,求證:![]() ;
;
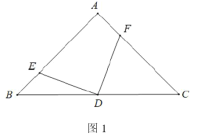
(2)如圖2,求![]() 的值(含
的值(含![]() 的式子表示);
的式子表示);
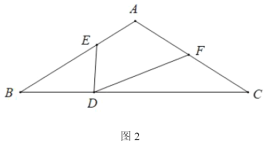
(3)如圖3,連接![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,直接寫出
,直接寫出![]() 的值為______.
的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
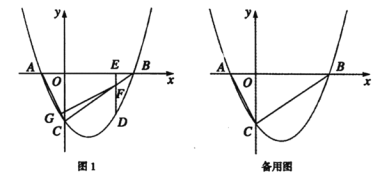
【題目】如圖1,拋物線![]()
![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,且
,且![]() .
.
(1)求該拋物線的函數表達式;
(2)動點![]() 在線段
在線段![]() 下方的拋物線上.
下方的拋物線上.
①連接![]() 、
、![]() ,過點
,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,交
,交![]() 于點
于點![]() .過點
.過點![]() 作
作![]() ,垂足為
,垂足為![]() .設點
.設點![]() 的橫坐標為
的橫坐標為![]() ,線段
,線段![]() 的長為
的長為![]() ,用含
,用含![]() 的代數式表示
的代數式表示![]() ;
;
②過點![]() 作
作![]() ,垂足為
,垂足為![]() ,連接
,連接![]() .是否存在點
.是否存在點![]() ,使得
,使得![]() 中的一個角恰好等于
中的一個角恰好等于![]() 的2倍?如果存在,求出點
的2倍?如果存在,求出點![]() 的橫坐標;如果不存在,請說明理由.
的橫坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2019·信陽一模)如圖,銳角三角形ABC中,BC=6,BC邊上的高為4,直線MN交邊AB于點M,交AC于點N,且MN∥BC,以MN為邊作正方形MNPQ,設其邊長為x(x>0),正方形MNPQ與△ABC公共部分的面積為y,則y與x的函數圖象大致是( )

A.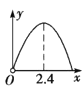 B.
B. C.
C.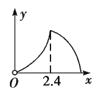 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=45°,將△ABC繞點A逆時針方向旋轉得△AEF,其中,E,F是點B,C旋轉后的對應點,BE,CF相交于點D.若四邊形ABDF為菱形,則∠CAE的大小是( )
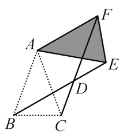
A.90°B.75°C.60°D.45°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A坐標為(0,3),點B在x軸上
(1)在坐標系中求作一點M,使得點M到點A,點B和原點O這三點的距離相等,在圖中保留作圖痕跡,不寫作法;
(2)若sin∠OAB=![]() ,求點M的坐標;
,求點M的坐標;
(3)在(2)的條件下,直接寫出以點O、M、B為其中三個頂點的平行四邊形的第四個頂點P的坐標

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某中學九年級數學活動小組選定測量學校前面小河對岸大樹BC的高度,他們在斜坡上D處測得大樹頂端B的仰角是30°,朝大樹方向下坡走6米到達坡底A處,在A處測得大樹頂端B的仰角是48°.若斜坡FA的坡比i=1:![]() ,求大樹的高度.(結果保留一位小數)參考數據:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大樹的高度.(結果保留一位小數)參考數據:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() 取1.73.
取1.73.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com