
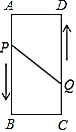
【題目】如圖,長方形![]() 中,
中,![]() ,
,![]() ,動點
,動點![]() 、
、![]() 分別從點
分別從點![]() 、
、![]() 同時出發,點
同時出發,點![]() 以2厘米/秒的速度向終點
以2厘米/秒的速度向終點![]() 移動,點
移動,點![]() 以1厘米/秒的速度向
以1厘米/秒的速度向![]() 移動,當有一點到達終點時,另一點也停止運動.設運動的時間為
移動,當有一點到達終點時,另一點也停止運動.設運動的時間為![]() 秒,當
秒,當![]() ________時,以點
________時,以點![]() 、
、![]() 、
、![]() 為頂點的三角形是等腰三角形.
為頂點的三角形是等腰三角形.
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
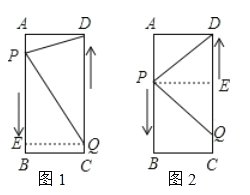
分情況討論,如圖1,當PQ=DQ時,如圖2,當PD=PQ時,如圖3,當PD=QD時,由等腰三角形的性質及勾股定理建立方程就可以得出結論.
解:如圖1,當PQ=DQ時,作QE⊥AB于E,
∴∠PEQ=90°,
∵∠B=∠C=90°,
∴四邊形BCQE是矩形,
∴QE=BC=2cm,BE=CQ=t.
∵AP=2t,
∴PE=6﹣2t﹣t=6﹣3t.DQ=6﹣t.
∵PQ=DQ,
∴PQ=6﹣t.
在Rt![]() PQE中,由勾股定理,得
PQE中,由勾股定理,得
(6﹣3t)2+4=(6﹣t)2,
解得:t=![]() .
.
如圖2,當PD=PQ時,
作PE⊥DQ于E,
∴DE=QE=![]() DQ,∠PED=90°.
DQ,∠PED=90°.
∵∠B=∠C=90°,
∴四邊形BCQE是矩形,
∴PE=BC=2cm.
∵DQ=6﹣t,
∴DE=![]() .
.
∴2t=![]() ,
,
解得:t=![]() ;
;
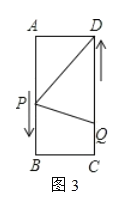
如圖5,當PD=QD時,
∵AP=2t,CQ=t,
∴DQ=6﹣t,
∴PD=6﹣t.
在Rt![]() APD中,由勾股定理,得
APD中,由勾股定理,得
4+4t2=(6﹣t)2,
解得t1=![]() ,t2=
,t2=![]() (舍去).
(舍去).
綜上所述:t=![]() ,
,![]() ,
,![]() ,
,![]() .
.
故答案為:![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
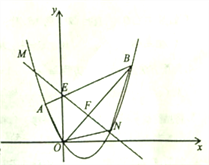
【題目】(12分)如圖,平面直角坐標系![]() 中點
中點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,拋物線經過
,拋物線經過![]() 、
、![]() 、
、![]() 三點,連接
三點,連接![]() ,線段
,線段![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求拋物線的函數解析式;
(3)點![]() 為線段
為線段![]() 上的一個動點(不與點
上的一個動點(不與點![]() 、
、![]() 重合),直線
重合),直線![]() 與拋物線交于
與拋物線交于![]() 、
、![]() 兩點(點
兩點(點![]() 在
在![]() 軸右側),連接
軸右側),連接![]() ,當四邊形
,當四邊形![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標并求出四邊形
的坐標并求出四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為6的等邊三角形ABC中,D是AB邊上的一動點,由A向B運動(A、B不重合),F是BC延長線上的一動點,與D同時以相同的速度由C向BC延長線方向運動(與C不重合),過點D作DE⊥AC,連接DF交AC于G.
(1)當點D運動到AB的中點時,直接寫出AE的長.
(2)當DF⊥AB時,求AD的長.
(3)在運動過程中線段GE的長是否發生變化?如果不變,求出線段GE的長:如果發生改變請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
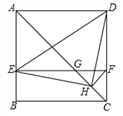
【題目】如圖,在正方形ABCD中,AC為對角線,E為AB上一點,過點E作![]() ,與AC、DC分別交于點
,與AC、DC分別交于點![]() 為CG的中點,連結DE、EH、DH、
為CG的中點,連結DE、EH、DH、![]() 下列結論:
下列結論: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,則
,則![]() 其中結論正確的有
其中結論正確的有![]()
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
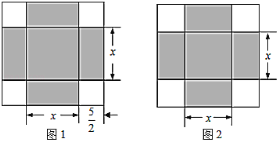
【題目】《代數學》中記載,形如![]() 的方程,求正數解的幾何方法是:“如圖1,先構造一個面積為
的方程,求正數解的幾何方法是:“如圖1,先構造一個面積為![]() 的正方形,再以正方形的邊長為一邊向外構造四個面積為
的正方形,再以正方形的邊長為一邊向外構造四個面積為![]() 的矩形,得到大正方形的面積為
的矩形,得到大正方形的面積為![]() ,則該方程的正數解為
,則該方程的正數解為![]() .”小聰按此方法解關于
.”小聰按此方法解關于![]() 的方程
的方程![]() 時,構造出如圖2所示的圖形,已知陰影部分的面積為36,則該方程的正數解為( )
時,構造出如圖2所示的圖形,已知陰影部分的面積為36,則該方程的正數解為( )
A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據如表回答下列問題:
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(1)275.56的平方根是______ ;
(2)![]() = ______ ;
= ______ ;
(3)查看上表, <![]() < .
< .
查看答案和解析>>
科目:初中數學 來源: 題型:
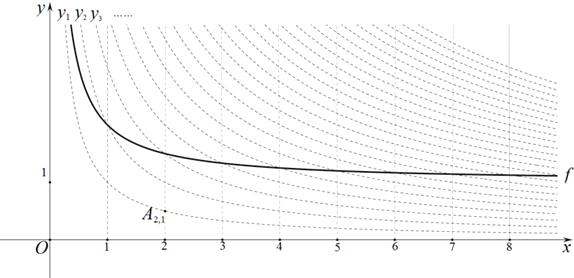
【題目】如圖,在平面直角坐標系xOy中,定義直線![]() 與雙曲線
與雙曲線![]() 的交點
的交點![]() 、n為正整數
、n為正整數![]() 為“雙曲格點”,雙曲線
為“雙曲格點”,雙曲線![]() 在第一象限內的部分沿著豎直方向平移或以平行于x軸的直線為對稱軸進行翻折之后得到的函數圖象為其“派生曲線”.
在第一象限內的部分沿著豎直方向平移或以平行于x軸的直線為對稱軸進行翻折之后得到的函數圖象為其“派生曲線”.
![]() “雙曲格點”
“雙曲格點”![]() 的坐標為______;
的坐標為______; ![]() 若線段
若線段![]() 的長為1個單位長度,則
的長為1個單位長度,則![]() ______;
______;
![]() 圖中的曲線f是雙曲線
圖中的曲線f是雙曲線![]() 的一條“派生曲線”,且經過點
的一條“派生曲線”,且經過點![]() ,則f的解析式為
,則f的解析式為![]() ______;
______;
![]() 畫出雙曲線
畫出雙曲線![]() 的“派生曲線”
的“派生曲線”![]() 與雙曲線
與雙曲線![]() 不重合
不重合![]() ,使其經過“雙曲格點”
,使其經過“雙曲格點”![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】.如圖,一條生產線的流水線上依次有5個機器人,它們站立的位置在數軸上依次用點A1,A2,A3,A4,A5表示.

(1)若原點是零件的供應點,5個機器人分別到供應點取貨的總路程是多少?
(2)若將零件的供應點改在A1,A3,A5中的其中一處,并使得5個機器人分別到達供應點取貨的總路程最短,你認為應該在哪個點上?通過計算說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com