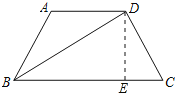
【題目】梯形ABCD中，AD∥BC，AB=DC=2
，∠DBC=30°，∠BDC=90°，求：梯形ABCD的面積．
【答案】9
．
【解析】
試題分析：作DE⊥BCTVE，則∠DEB=90°，由含30°角的直角三角形的性質得出DE=
BD，BC=2DC=4
，求出BD=DC=6，DE=3，由等腰梯形的性質得出∠ABD=∠ADB，得出AD=AB=2，即可求出梯形ABCD的面積．
解：如圖所示：
作DE⊥BCTVE，則∠DEB=90°，
∵∠DBC=30°，∠BDC=90°，
∴∠C=60°，DE=BD，BC=2DC=4，BD=DC=6，
∴DE=3，
∵AD∥BC，AB=DC，
∴∠ABC=∠C=60°，∠ADB=∠BDC=30°，
∴∠ABD=30°=∠ADB，
∴AD=AB=2，
∴梯形ABCD的面積=（AD+BC）×DE=
（2+4）×3=9．
科目：初中數學 來源： 題型：
【題目】今年我國西南五省市發生旱災，尤其是西藏受災最為嚴重，經濟損失已經超過170億，那么170億用科學記數法表示為____________________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在直角坐標系中，矩形OABC的頂點O與坐標原點重合，頂點A，C分別在坐標軸上，頂點B的坐標為，過點D和E的直線分別與AB，BC交于點M，N。
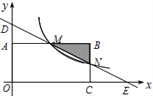
（1）、求直線DE的解析式和點M的坐標；
（2）、若反比例函數y=
的圖象經過點M，求該反比例函數的解析式，并通過計算判斷點N是否在該函數的圖象上；
（3）、若反比例函數的圖象與△MNB有公共點，請直接寫出m的取值范圍。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等邊△ABC內有一點D，AD=5，BD=6，CD=4，將△ABD繞A點逆時針旋轉，使AB與AC重合，點D旋轉至點E，求∠CDE的余弦值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用四舍五入法對2.06032分別取近似值，其中錯誤的是（ ）
A. 2.1（精確到0.1） B. 2.06（精確到千分位）
C. 2.06（精確到百分位） D. 2.0603（精確到0.0001）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com