
【題目】如圖,在平面直角坐標系![]() 中,已知△ABC和△DEF的頂點分別為A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
中,已知△ABC和△DEF的頂點分別為A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
按下列要求畫圖:以點O為位似中心,將△ABC向y軸左側按比例尺2:1放大得△ABC的位似圖形△A1B1C1,并解決下列問題:
(1)頂點A1的坐標為 ,B1的坐標為 ,C1的坐標為 ;
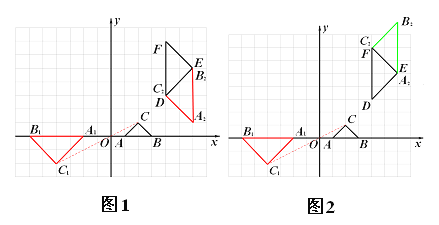
(2)請你利用旋轉、平移兩種變換,使△A1B1C1通過變換后得到△A2B2C2,且△A2B2C2恰與△DEF拼接成一個平行四邊形(非正方形),寫出符合要求的變換過程.

【答案】見解析
【解析】解:作圖如下:
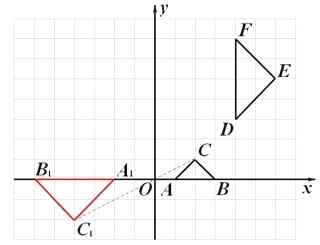
(1)(-2,0),(-6,0),(-4,-2)。
(2)符合要求的變換有兩種情況:
情況1:如圖1,變換過程如下:
將△A2B2C2向右平移12個單位,再向上平移5個單位;再以B1為中心順時針旋轉900。
情況2:如圖2,變換過程如下:
將△A2B2C2向右平移8個單位,再向上平移5個單位;再以A1為中心順時針旋轉900。
(1)作位似變換的圖形的依據是相似的性質,基本作法是:①先確定圖形的位似中心;②利用相似圖形的比例關系作出關鍵點的對應點;③按原圖形中的方式順次連接對應點.要注意有兩種情況,圖形在位似中心的同側或在位似中心的兩側。
(2)作平移變換時,找關鍵點的對應點也是關鍵的一步.平移作圖的一般步驟為:①確定平移的方向和距離,先確定一組對應點;②確定圖形中的關鍵點;③利用第一組對應點和平移的性質確定圖中所有關鍵點的對應點;④按原圖形順序依次連接對應點,所得到的圖形即為平移后的圖形。
作旋轉變換時,找準旋轉中心和旋轉角度


科目:初中數學 來源: 題型:
【題目】計算題:
(1)(-20)+(+3)+(-5)+(+7);
(2)16-(-15)-4+(-5);
(3)(-12)×(-37)×![]() ;
;
(4)(-![]() )÷
)÷![]() ÷(-
÷(-![]() );
);
(5)-30×(![]()
![]()
![]() );
);
(6)-3-[-5 +(1-![]() ×0.6)÷(-3)]
×0.6)÷(-3)]
(7)![]()
(8)![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
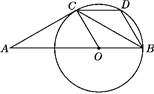
【題目】如圖,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一點O,使OB=OC,以點O為圓心,OB為半徑作圓,過點C作CD∥AB交⊙O于點D,連接BD.
(1)猜想AC與⊙O的位置關系,并證明你的猜想;
(2)試判斷四邊形BOCD的形狀,并證明你的判斷;
(3)已知AC=6,求扇形OBC所圍成的圓錐的底面圓的半徑r.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖![]() ,
,![]() 分別為數軸上的兩點,
分別為數軸上的兩點,![]() 點對應的數為-10,
點對應的數為-10,![]() 點對應的數為90.
點對應的數為90.

(1)![]() ,
,![]() 兩點間的距離為________.
兩點間的距離為________.
(2)現在有一只電子螞蟻![]() 從
從![]() 點出發,以2個單位/秒的速度向右運動,同時另一只電子螞蟻
點出發,以2個單位/秒的速度向右運動,同時另一只電子螞蟻![]() 恰好從
恰好從![]() 點出發,以3個單位/秒的速度向左運動.運動時間為
點出發,以3個單位/秒的速度向左運動.運動時間為![]() 秒,用含
秒,用含![]() 的代數式表示:
的代數式表示:
①點![]() 在數軸上表示的數為________.
在數軸上表示的數為________.
②若兩只電子螞蟻在數軸上的![]() 點相遇,則
點相遇,則![]() 點對應的數是多少.
點對應的數是多少.
(3)若當電子螞蟻![]() 從
從![]() 點出發時,以4個單位/秒的速度向左運動,同時另一只電子螞蟻
點出發時,以4個單位/秒的速度向左運動,同時另一只電子螞蟻![]() 恰好從
恰好從![]() 點出發,以6個單位/秒的速度向左運動,經過多長的時間兩只電子螞蟻在數軸上相距20個單位長度.
點出發,以6個單位/秒的速度向左運動,經過多長的時間兩只電子螞蟻在數軸上相距20個單位長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O 中,AB為直徑,CD為⊙O的切線,交AB的延長線于點D,∠D=30°.(1)求∠A的度數;(2)若點F在⊙O上,CF⊥AB,垂足為E,CF=4![]() ,求圖中陰影部分的面積.(結果保留π)
,求圖中陰影部分的面積.(結果保留π)

查看答案和解析>>
科目:初中數學 來源: 題型:
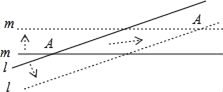
【題目】根據愛因斯坦的相對論可知,任何物體的運動速度不能超過光速(3×105km/s),因為一個物體達到光速需要無窮多的能量,并且時光會倒流,這在現實中是不可能的.但我們可讓一個虛擬物超光速運動,例如:直線l,m表示兩條木棒相交成的銳角的度數為10°,它們分別以與自身垂直的方向向兩側平移時,它們的交點A也隨著移動(如圖箭頭所示),如果兩條直線的移動速度都是光速的0.2倍,則交點A的移動速度是光速的_____倍.(結果保留兩個有效數字).
查看答案和解析>>
科目:初中數學 來源: 題型:
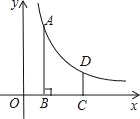
【題目】如圖,在平面直角坐標系中,反比例函數y=![]() (x>0)的圖象上有一點A(m,4),過點A作AB⊥x軸于點B,將點B向右平移2個單位長度得到點C,過點C作y軸的平行線交反比例函數的圖象于點D.
(x>0)的圖象上有一點A(m,4),過點A作AB⊥x軸于點B,將點B向右平移2個單位長度得到點C,過點C作y軸的平行線交反比例函數的圖象于點D.
(1)點D的橫坐標為_____(用戶含m的代數式表示).
(2)當CD=![]() 時,求反比例函數所對應的函數表達式.
時,求反比例函數所對應的函數表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com