【題目】如圖所示．
（1）已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，求∠MON的度數；
（2）∠AOB=α，∠BOC=β，OM平分∠AOC，ON平分∠BOC，求∠MON的大小．
【答案】（1）45°；（2）
α
【解析】試題分析：（1）先求得∠AOC的度數，然后再依據角平分線的定義求得∠COM和∠NOC的度數，最后，再依據∠MON=∠MOC﹣∠CON求解即可；
（2）按照（1）中的方法和思路求解即可．
試題解析：解：（1）∵∠AOB=90°，∠BOC=30°，∴∠AOC=∠AOB+∠BOC=90°+30°=120°．
∵OM平分∠AOC，ON平分∠BOC，∴∠MOC= 
∠AOC=60°，∠CON=
∠BOC=15°，∴∠MON=∠MOC﹣∠CON=60°﹣15°=45°．
（2）同理可得，∠MOC=
（α+β），∠CON=
β．
則∠MON=∠MOC﹣∠CON=
（α+β）﹣
β=
α．
奪冠訓練單元期末沖刺100分系列答案
新思維小冠軍100分作業本系列答案
名師指導一卷通系列答案科目：初中數學 來源： 題型：
【題目】如圖1，A，B分別在射線OA，ON上，且∠MON為鈍角，現以線段OA，OB為斜邊向∠MON的外側作等腰直角三角形，分別是△OAP，△OBQ，點C，D，E分別是OA，OB，AB的中點．
（1）求證：△PCE≌△EDQ；
（2）延長PC，QD交于點R．如圖2，若∠MON=150°，求證：△ABR為等邊三角形；
（3）如圖3，若△ARB∽△PEQ，求∠MON大小.
查看答案和解析>>
科目：初中數學 來源： 題型：
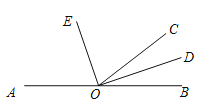
【題目】如圖，已知點O是直線AB上的一點， 
，OD、OE分別是
、
的角平分線．
（1）求
的度數；
（2）寫出圖中與
互余的角；
（3）圖中有
的補角嗎？若有，請把它找出來，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列算式：12-02=1+0=1，,22-12=2+1=3,32-22=3+2=5,42-32=4+3=7 ，52-42=5+4=9，…….
若字母 
表示自然數，請把你觀察到的規律用含有 
的式子表示出來________．
查看答案和解析>>
科目：初中數學 來源： 題型：
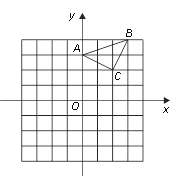
【題目】已知：△ABC在坐標平面內，三個頂點的坐標分別為A（0，3），B（3，4），C（2，2）.（正方形網格中， 每個小正方形的邊長是1個單位長度）
（1）畫出△ABC向下平移4個單位得到的△A1B1C1，并直接寫出C1點的坐標；
（2）以點B為位似中心，在網格中畫出△A2BC2，使△A2BC2與△ABC位似，且位似比為2︰1，并直接寫出C2點的坐標及△A2BC2的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列條件中，不能判斷四邊形ABCD是平行四邊形的是（ ）
A.∠A=∠C，∠B=∠D
B.AB∥CD，AB=CD
C.AB=CD，AD∥BC
D.AB∥CD，AD∥BC
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠BAC＝30°，以AB為直徑的⊙O經過點C.過點C作⊙O的切線交AB的延長線于點P.點D為圓上一點，且
，弦AD的延長線交切線PC于點E，連接BC．
（1）判斷OB和BP的數量關系,并說明理由；
（2）若⊙O的半徑為2，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果三條線段之比是：（1）2：2：3；（2）2：3：5；（3）1：4：6；（4）3：4：5，其中能構成三角形的有（ ）
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com