
【題目】如圖,在△ABC中,∠C=90°,以AB上一點O為圓心,OA長為半徑的圓與BC相切于點D,分別交AC、AB于點E、F. 
(1)若AC=6,AB=10,求⊙O的半徑;
(2)連接OE、ED、DF、EF.若四邊形BDEF是平行四邊形,試判斷四邊形OFDE的形狀,并說明理由.
【答案】
(1)解:連接OD.設⊙O的半徑為r.
∵BC切⊙O于點D,
∴OD⊥BC.
∵∠C=90°,
∴OD∥AC,
∴△OBD∽△ABC.
∴ ![]() =
= ![]() ,即10r=6(10﹣r).
,即10r=6(10﹣r).
解得r= ![]() ,
,
∴⊙O的半徑為 ![]()
(2)解:四邊形OFDE是菱形.理由如下:
∵四邊形BDEF是平行四邊形,
∴∠DEF=∠B.
∵∠DEF= ![]() ∠DOB,
∠DOB,
∴∠B= ![]() ∠DOB.
∠DOB.
∵∠ODB=90°,
∴∠DOB+∠B=90°,
∴∠DOB=60°.
∵DE∥AB,
∴∠ODE=60°.
∵OD=OE.
∴OD=DE.
∵OD=OF,
∴DE=OF.
又∵DE∥OF,
∴四邊形OFDE是平行四邊形.
∵OE=OF,
∴平行四邊形OFDE是菱形.

【解析】(1)連接OD,設⊙O的半徑為r,可證出△BOD∽△BAC,則 ![]() =
= ![]() ,從而求得r;(2)由四邊形BDEF是平行四邊形,得∠DEF=∠B,再由圓周角定理可得,∠B=
,從而求得r;(2)由四邊形BDEF是平行四邊形,得∠DEF=∠B,再由圓周角定理可得,∠B= ![]() ∠DOB,則△ODE是等邊三角形,先得出四邊形OFDE是平行四邊形.再根據OE=OF,則平行四邊形OFDE是菱形.
∠DOB,則△ODE是等邊三角形,先得出四邊形OFDE是平行四邊形.再根據OE=OF,則平行四邊形OFDE是菱形.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對平行四邊形的性質的理解,了解平行四邊形的對邊相等且平行;平行四邊形的對角相等,鄰角互補;平行四邊形的對角線互相平分.


科目:初中數學 來源: 題型:
【題目】從今年起,我市生物和地理會考實施改革,考試結果以等級形式呈現,分A、B、C、D四個等級.某校八年級為了迎接會考,進行了一次模擬考試,隨機抽取部分學生的生物成績進行統計,繪制成如下兩幅不完整的統計圖.
(1)這次抽樣調查共抽取了名學生的生物成績.扇形統計圖中,D等級所對應的扇形圓心角度數為°;
(2)將條形統計圖補充完整;
(3)如果該校八年級共有600名學生,請估計這次模擬考試有多少名學生的生物成績等級為D?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了解本校學生對球類運動的愛好情況,采用抽樣的方法,從足球、籃球、排球、其它等四個方面調查了若干名學生,并繪制成“折線統計圖”與“扇形統計圖”.請你根據圖中提供的部分信息解答下列問題: 

(1)在這次調查活動中,一共調查了名學生;
(2)“足球”所在扇形的圓心角是度;
(3)補全折線統計圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某品牌太陽能熱水器的實物圖和橫斷面示意圖,已知真空集熱管與支架CD所在直線相交于水箱橫斷面⊙O的圓心O,支架CD與水平面AE垂直,AB=150厘米,∠BAC=30°,另一根輔助支架DE=76厘米,∠CED=60°. 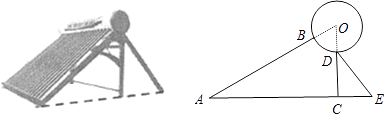
(1)求垂直支架CD的長度;(結果保留根號)
(2)求水箱半徑OD的長度.(結果保留三個有效數字,參考數據: ![]() ≈1.414,
≈1.414, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將邊長為 ![]() 的正方形ABCD沿對角線AC平移,使點A移至線段AC的中點A′處,得新正方形A′B′C′D′,新正方形與原正方形重疊部分(圖中陰影部分)的面積是( )
的正方形ABCD沿對角線AC平移,使點A移至線段AC的中點A′處,得新正方形A′B′C′D′,新正方形與原正方形重疊部分(圖中陰影部分)的面積是( ) 
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,PA,PB是⊙O的兩條切線,切點分別為A,B,OP交AB于點C,OP=13,sin∠APC= ![]() .
. 
(1)求⊙O的半徑;
(2)求弦AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學學生為了解該校學生喜歡球類活動的情況,隨機抽取了若干名學生進行問卷調查(要求每位學生只能填寫一種自己喜歡的球類),并將調查的結果繪制成如下的兩幅不完整的統計圖. 
請根據圖中提供的信息,解答下面的問題:
(1)參加調查的學生共有人,在扇形圖中,表示“其他球類”的扇形的圓心角為度;
(2)將條形圖補充完整;
(3)若該校有2000名學生,則估計喜歡“籃球”的學生共有人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com