
【題目】如圖1,在平面直角坐標系中,點![]() 、
、![]() ,將
,將![]() 沿
沿![]() 軸翻折得到
軸翻折得到![]() ,已知拋物線
,已知拋物線![]() 過點
過點![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
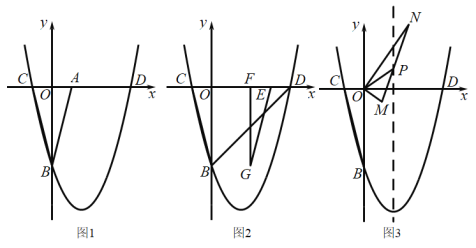
(1)拋物線頂點的坐標為_______;
(2)如圖2,![]() 沿
沿![]() 軸向右以每秒
軸向右以每秒![]() 個單位長度的速度平移得到
個單位長度的速度平移得到![]() ,運動時間為
,運動時間為![]() 秒.當
秒.當![]() 時,求
時,求![]() 與
與![]() 重疊面積
重疊面積![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)如圖3,將![]() 繞點
繞點![]() 順時針旋轉得到
順時針旋轉得到![]() ,線段
,線段![]() 與拋物線對稱軸交于點
與拋物線對稱軸交于點![]() .在旋轉一圈過程中,是否存在點
.在旋轉一圈過程中,是否存在點![]() ,使得
,使得![]() ?若存在,直接寫出所有滿足條件的點
?若存在,直接寫出所有滿足條件的點![]() 的坐標;若不存在,試說明理由.
的坐標;若不存在,試說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,(
;(3)存在,(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)由軸對稱可得點B、C坐標,可求得拋物線解析式,進而得到拋物線頂點坐標;
(2)根據題意構造相似三角形,用t表示對于線段,再用割補法表示![]() 與
與![]() 重疊面積即可;
重疊面積即可;
(3)由題意可知,點P為線段MN中點,由拋物線性質,求得P點坐標,設出M(m,n)坐標,再由三角形相似可得N點坐標,用中點坐標公式可表示P點坐標,構造方程可求m,n,則問題可解.
解:(1)由已知,點C坐標為(-1,0)
把(-1,0),(0,-4)代入![]() ,得
,得
![]()
解得,![]()
∴![]()
則對稱軸為直線![]()
頂點縱坐標為:![]()
∴ 頂點坐標為![]()
故答案為:![]()
(2)連BG,設BD交GE于點K,BD交FG于 T,過K做HK⊥FG于H

由(1)可知,點D坐標為(4,0)
則![]()
由已知,![]() ,
,
∵GB∥OD
∴![]()
則有![]() ,則
,則![]() ,
,
得:![]()
![]() ,
,
![]()
![]()
(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
如圖,當M在第四象限時,根據題意可知:當點![]() 是
是![]() 中點時,
中點時,![]()
∴MN=BC=![]()
則![]() ,
,
P到x軸距離為: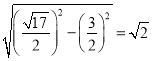
可得:![]()
分別過點M、N作MF⊥y軸于點F,NE⊥y軸于點E
![]()
0
∵![]()
∴![]()
∵![]()
∴![]()
![]()
∴設![]() ,則
,則![]() ,
,
∴點P坐標為(![]() ,
,![]() )
)
∴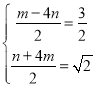
解得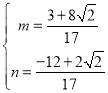
∴M坐標為(![]() ,
,![]() )
)
當點M在第三象限時,同理,設![]() ,則
,則![]()
∴點P坐標為(![]() ,
,![]() )
)
同理點![]()
∴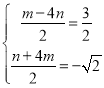
解得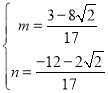
∴M坐標為(![]() ,
,![]() )
)
故答案為(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)


科目:初中數學 來源: 題型:
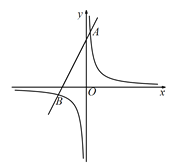
【題目】如圖,在平面系中,一次函數![]() 的圖像經過定點A,反比例函數
的圖像經過定點A,反比例函數![]() 的圖像經過點A,且與一次函數
的圖像經過點A,且與一次函數![]() 的圖像相交于點B(
的圖像相交于點B(![]() ,m).
,m).
(1)求m、a的值;
(2)設橫坐標為n的點P在反比例函數圖象的第三象限上,且在點B右側,連接AP、BP,△ABP的面積為12,求代數式![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】化簡:![]() +
+![]() +…+
+…+![]() .
.
為了能找到復雜計算問題的結果,我們往往會通過將該問題分解,試圖找尋算式中每個式子是否存在某種共同規律,然后借助這個規律將問題轉化為可以解決的簡單問題.下面我們嘗試著用這個思路來解決上面的問題.請你按照這個思路繼續進行下去,并把相應橫線上的空格補充完整.
(分析問題)第1個加數:![]() =
=![]() ﹣
﹣![]() ;
;
第2個加數:![]() =
=![]() ﹣
﹣![]() ;
;
第3個加數:![]() =
=![]() ﹣
﹣![]() ;
;
第4個加數: =![]() ﹣
﹣![]() ;
;
(總結規律)第n個加數: = ﹣ .
(解決問題)請你利用上面找到的規律,繼續化簡下面的問題.(結果只需化簡,無需求出最后得數)![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】揚州包子是淮揚菜系的維揚點心代表,里面的餡品種豐富.早飯準備了四個包子,一個蟹黃包、一個松籽包、兩個三鮮包,四個包子除餡外其他都相同.
(1)請預測“吃一個包子恰好是松籽包”的概率是_______;
(2)請用畫樹狀圖或用表格的方法預測“吃兩個包子恰好是三鮮包”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于二次函數![]() ,以下結論:①拋物線交
,以下結論:①拋物線交![]() 軸有兩個不同的交點;②不論
軸有兩個不同的交點;②不論![]() 取何值,拋物線總是經過一個定點;③設拋物線交
取何值,拋物線總是經過一個定點;③設拋物線交![]() 軸于
軸于![]() 、
、![]() 兩點,若
兩點,若![]() ,則
,則![]() ;④拋物線的頂點在
;④拋物線的頂點在![]() 圖象上;⑤拋物線交
圖象上;⑤拋物線交![]() 軸于
軸于![]() 點,若
點,若![]() 是等腰三角形,則
是等腰三角形,則![]() ,
,![]() ,
,![]() .其中正確的序號是( )
.其中正確的序號是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校隨機對本校部分學生進行“假期中,我在家可以這么做:![]() .扎實學習、
.扎實學習、![]() .快樂游戲、
.快樂游戲、![]() .經典閱讀、
.經典閱讀、![]() .分擔勞動、
.分擔勞動、![]() .樂享健康”網絡調查,并根據調查結果繪制成如下兩幅不完整的統計圖(若每一位同學只能選擇一項),請根據圖中信息,回答下列問題.
.樂享健康”網絡調查,并根據調查結果繪制成如下兩幅不完整的統計圖(若每一位同學只能選擇一項),請根據圖中信息,回答下列問題.

(1)這次調查的總人數是___________人;
(2)請補全條形統計圖,并說明扇形統計圖中![]() 所對應的圓心角是___________度;
所對應的圓心角是___________度;
(3)若該學校共有學生1700人,則選擇![]() 有多少人?
有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O.
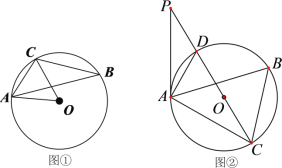
(1)如圖①,連接OA,OC,若![]() ,求
,求![]() 的度數;
的度數;
(2)如圖②,直徑CD的延長線與過點A的切線相交于點P.若![]() ,⊙O的半徑為2,求AD,PD的長.
,⊙O的半徑為2,求AD,PD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com