
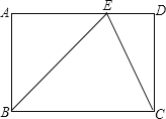
【題目】如圖,在矩形ABCD中,點E在AD上,且EC平分∠BED.
(1)△BEC是否為等腰三角形?證明你的結論;
(2)若AB=2,∠DCE=22.5°,求BC長.
【答案】(1)△BEC是等腰三角形,見解析;(2)2![]()
【解析】
(1)由矩形的性質和角平分線的定義得出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)證出AE=AB=2,根據勾股定理求出BE,即可得出BC的長.
解:(1)△BEC是等腰三角形;理由如下:
∵四邊形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠BCE,
∵EC平分∠DEB,
∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC,即△BEC是等腰三角形.
(2)∵四邊形ABCD是矩形,
∴∠A=∠D=90°,
∵∠DCE=22.5°,
∴∠DEB=2×(90°-22.5°)=135°,
∴∠AEB=180°-∠DEB=45°,
∴∠ABE=∠AEB=45°,
∴AE=AB=2,
由勾股定理得:BC=BE=![]() =
=![]() =2
=2![]() ,
,
答:BC的長是2![]() .
.


科目:初中數學 來源: 題型:
【題目】汽車油箱中的余油量![]() (升)隨汽車行駛的時間
(升)隨汽車行駛的時間![]() (時)的變化而變化,
(時)的變化而變化,![]() 與
與![]() 之間的關系為
之間的關系為![]() ,其中
,其中![]() 是油箱中原有的油的升數,若這輛汽車油箱中原有油60升.
是油箱中原有的油的升數,若這輛汽車油箱中原有油60升.
(1)用表格表示行駛1到5小時過程中這輛汽車油箱中余油量與行駛時間![]() 的關系,填寫下表:
的關系,填寫下表:
行駛時間(時) | 1 | 2 | 3 | 4 | 5 |
余油量(升) |
(2)這輛車最多可行駛多少小時?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面內的兩條直線有相交和平行兩種位置關系
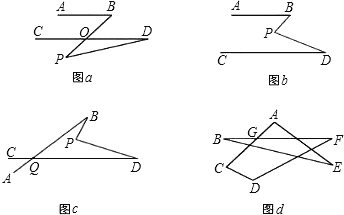
(1)如圖a,若AB∥CD,點P在AB、CD外部,則有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.將點P移到AB、CD內部,如圖b,以上結論是否成立?若成立,說明理由;若不成立,則∠BPD、∠B、∠D之間有何數量關系?請證明你的結論;
(2)在圖b中,將直線AB繞點B逆時針方向旋轉一定角度交直線CD于點Q,如圖c,則∠BPD、∠B、∠D、∠BQD之間有何數量關系?(不需證明)
(3)根據(2)的結論求圖d中∠A+∠B+∠C+∠D+∠E+∠F的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大家看過中央電視臺“購物街”節目嗎?其中有一個游戲環節是大轉輪比賽,轉輪上平均分布著5、10、15、20一直到100共20個數字.選手依次轉動轉輪,每個人最多有兩次機會.選手轉動的數字之和最大不超過100者為勝出;若超過100則成績無效,稱為“爆掉”.
(1)某選手第一次轉到了數字5,再轉第二次,則他兩次數字之和為100的可能性有多大?
(2)現在某選手第一次轉到了數字65,若再轉第二次了則有可能“爆掉”,請你分析“爆掉”的可能性有多大?
查看答案和解析>>
科目:初中數學 來源: 題型:
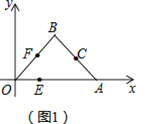
【題目】已知:如(圖1),在平面直角坐標中,A(12,0),B(6,6),點C為線段AB的中點,點D與原點O關于點C對稱.
(1)利用直尺和圓規在(圖1)中作出點D的位置(保留作圖痕跡),判斷四邊形OBDA的形狀,并說明理由;
(2)在(圖1)中,動點E從點O出發,以每秒1個單位的速度沿線段OA運動,到達點A時停止;同時,動點F從點O出發,以每秒a個單位的速度沿OB→BD→DA運動,到達點A時停止.設運動的時間為t(秒).
①當t=4時,直線EF恰好平分四邊形OBDA的面積,求a的值;
②當t=5時,CE=CF,請直接寫出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
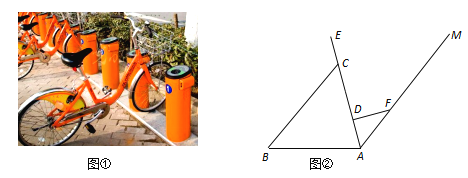
【題目】“低碳環保,你我同行”.近幾年,各大城市的公共自行車給市民出行帶來了極大的方便.圖①是公共自行車的實物圖,圖②是公共自行車的車架示意圖,點A.D、C、E在同一條直線上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于點D,座桿CE=15cm,且∠EAB=75°.
(1)求AD的長;
(2)求點E到AB的距離.(參考數據:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】教室里的飲水機接通電源就進入自動程序,開機加熱時每分鐘上升10℃,加熱到100℃,停止加熱,水溫開始下降,此時水溫(℃)與開機后用時(min)成反比例關系.直至水溫降至30℃,飲水機關機.飲水機關機后即刻自動開機,重復上述自動程序.若在水溫為30℃時,接通電源后,水溫y(℃)和時間(min)的關系如圖,為了在上午第一節下課時(8:45)能喝到不超過50℃的水,則接通電源的時間可以是當天上午的
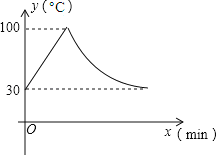
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中數學 來源: 題型:
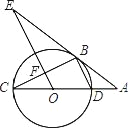
【題目】如圖,CD為⊙O的直徑,點B在⊙O上,連接BC、BD,過點B的切線AE與CD的延長線交于點A,OE∥BD,交BC于點F,交AE于點E.
(1)求證:△BEF∽△DBC.
(2)若⊙O的半徑為3,∠C=30°,求BE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com