
【題目】已知![]() ,
,![]() ,
,![]() ,斜邊
,斜邊![]() ,將
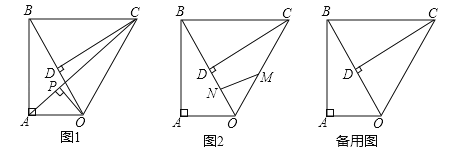
,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,如圖1,連接
,如圖1,連接![]() .
.
(1)填空:![]()
![]() ;
;
(2)如圖1,連接![]() ,作
,作![]() ,垂足為
,垂足為![]() ,求
,求![]() 的長度;
的長度;
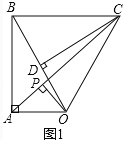
(3)如圖2,點![]() ,
,![]() 同時從點
同時從點![]() 出發(fā),在
出發(fā),在![]() 邊上運動,
邊上運動,![]() 沿
沿![]() 路徑勻速運動,
路徑勻速運動,![]() 沿
沿![]() 路徑勻速運動,當兩點相遇時運動停止,已知點
路徑勻速運動,當兩點相遇時運動停止,已知點![]() 的運動速度為1.5單位
的運動速度為1.5單位![]() 秒,點
秒,點![]() 的運動速度為1單位
的運動速度為1單位![]() 秒,設運動時間為
秒,設運動時間為![]() 秒,
秒,![]() 的面積為
的面積為![]() ,求當
,求當![]() 為何值時
為何值時![]() 取得最大值?最大值為多少?
取得最大值?最大值為多少?
【答案】(1)60;(2)![]() ;(3)x
;(3)x![]() 時,y有最大值,最大值
時,y有最大值,最大值![]() .
.
【解析】
(1)只要證明△OBC是等邊三角形即可;
(2)求出△AOC的面積,利用三角形的面積公式計算即可;
(3)分三種情形討論求解即可解決問題:①當0<x![]() 時,M在OC上運動,N在OB上運動,此時過點N作NE⊥OC且交OC于點E.②當
時,M在OC上運動,N在OB上運動,此時過點N作NE⊥OC且交OC于點E.②當![]() x≤4時,M在BC上運動,N在OB上運動.③當4<x≤4.8時,M、N都在BC上運動,作OG⊥BC于G.
x≤4時,M在BC上運動,N在OB上運動.③當4<x≤4.8時,M、N都在BC上運動,作OG⊥BC于G.
(1)由旋轉性質可知:OB=OC,∠BOC=60°,
∴△OBC是等邊三角形,
∴∠OBC=60°.
故答案為:60.
(2)如圖1中。
∵OB=4,∠ABO=30°,
∴OA![]() OB=2,AB
OB=2,AB![]() OA=2
OA=2![]() ,
,
∴S△AOC![]() OAAB
OAAB![]() 2×2
2×2![]() .
.
∵△BOC是等邊三角形,
∴∠OBC=60°,∠ABC=∠ABO+∠OBC=90°,
∴AC![]() ,
,
∴OP![]() .
.
(3)①當0<x![]() 時,M在OC上運動,N在OB上運動,此時過點N作NE⊥OC且交OC于點E.
時,M在OC上運動,N在OB上運動,此時過點N作NE⊥OC且交OC于點E.
則NE=ONsin60°![]() x,
x,
∴S△OMN![]() OMNE
OMNE![]() 1.5x
1.5x![]() x,
x,
∴y![]() x2,
x2,
∴x![]() 時,y有最大值,最大值
時,y有最大值,最大值![]() .
.
②當![]() x≤4時,M在BC上運動,N在OB上運動.
x≤4時,M在BC上運動,N在OB上運動.
作MH⊥OB于H.
則BM=8﹣1.5x,MH=BMsin60°![]() (8﹣1.5x),
(8﹣1.5x),
∴y![]() ON×MH
ON×MH![]() x2+2
x2+2![]() x.
x.
當x![]() 時,y取最大值,y
時,y取最大值,y![]() ,
,
③當4<x≤4.8時,M、N都在BC上運動,
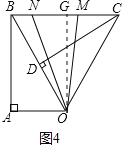
作OG⊥BC于G.MN=12﹣2.5x,OG=AB=2![]() ,
,
∴y![]() MNOG=12
MNOG=12![]() x,
x,
當x=4時,y有最大值,最大值=2![]() .
.
綜上所述:y有最大值,最大值為![]() .
.


 步步高達標卷系列答案
步步高達標卷系列答案科目:初中數(shù)學 來源: 題型:
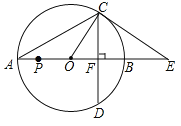
【題目】如圖,以AB為直徑的⊙O與CE相切于點C,CE交AB的延長線于點E,直徑AB=18,∠A=30°,弦CD⊥AB,垂足為點F,連接AC,OC,則下列結論正確的是______.(寫出所有正確結論的序號)
①![]() ;
;
②扇形OBC的面積為![]() π;
π;
③△OCF∽△OEC;
④若點P為線段OA上一動點,則APOP有最大值20.25.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,將點A向右平移6個單位長度,得到點B.
,將點A向右平移6個單位長度,得到點B.
(1)直接寫出點B的坐標;
(2)若拋物線y=-x2+bx+c經過點A,B,求拋物線的表達式;
(3)若拋物線y=-x2+bx+c的頂點在直線y=x+2上移動,當拋物線與線段AB有且只有一個公共點時,求拋物線頂點橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
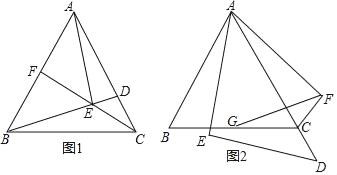
【題目】如圖,在等邊△ABC中,點D是AC邊上一點,連接BD,過點A作AE⊥BD于E.
(1)如圖1,連接CE并延長CE交AB于點F,若∠CBD=15°,AB=4,求CE的長;
(2)如圖2,當點D在線段AC的延長線上時,將線段AE繞點A逆時針旋轉60°得到線段AF,連接EF,交BC于G,連接CF,求證:BG=CG.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某公司購買了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的單價比
型芯片的單價比![]() 型芯片的單價少9元,已知該公司用3120元購買
型芯片的單價少9元,已知該公司用3120元購買![]() 型芯片的條數(shù)與用4200元購買
型芯片的條數(shù)與用4200元購買![]() 型芯片的條數(shù)相等.
型芯片的條數(shù)相等.
(1)求該公司購買的![]() 、
、![]() 型芯片的單價各是多少元?
型芯片的單價各是多少元?
(2)若兩種芯片共購買了200條,且購買的總費用為6280元,求購買了多少條![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】一天,小華和小夏玩擲骰子游戲,他們約定:他們用同一枚質地均勻的骰子各擲一次, 如果兩次擲的骰子的點數(shù)相同則小華獲勝:如果兩次擲的骰子的點數(shù)的和是6則小夏獲勝.
(1)請您列表或畫樹狀圖列舉出所有可能出現(xiàn)的結果;
(2)請你判斷這個游戲對他們是否公平并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
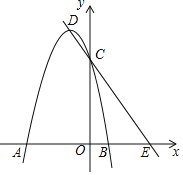
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+2ax﹣3a(a<0)與x軸相交于A,B兩點,與y軸相交于點C,頂點為D,直線DC與x軸相交于點E.
(1)當a=﹣1時,求拋物線頂點D的坐標,OE等于多少;
(2)OE的長是否與a值有關,說明你的理由;
(3)設∠DEO=β,45°≤β≤60°,求a的取值范圍;
(4)以DE為斜邊,在直線DE的左下方作等腰直角三角形PDE.設P(m,n),直接寫出n關于m的函數(shù)解析式及自變量m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小磊要制作一個三角形的鋼架模型,在這個三角形中,長度為x(單位:cm)的邊與這條邊上的高之和為40 cm,這個三角形的面積S(單位:cm2)隨x(單位:cm)的變化而變化.
(1)請直接寫出S與x之間的函數(shù)關系式(不要求寫出自變量x的取值范圍);
(2)當x是多少時,這個三角形面積S最大?最大面積是多少?![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
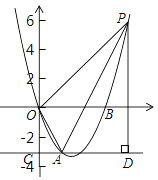
【題目】如圖,已知拋物線![]() 過點A(
過點A(![]() ,-3) 和B(3
,-3) 和B(3![]() ,0),過點A作直線AC//x軸,交y軸與點C.
,0),過點A作直線AC//x軸,交y軸與點C.
(1)求拋物線的解析式;
(2)在拋物線上取一點P,過點P作直線AC的垂線,垂足為D,連接OA,使得以A,D,P為頂點的三角形與△AOC相似,求出對應點P的坐標;
(3)拋物線上是否存在點Q,使得![]() ?若存在,求出點Q的坐標;若不存在,請說明理由.
?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com