【題目】已知一次函數y1＝kx＋b的圖像經過點（0，-2），（2，2）.
（1）求一次函數的表達式，并在所給直角坐標系中畫出此函數的圖像；；
（2）根據圖像回答：當x 時，y1=0；
（3）求直線y1＝kx＋b、直線y2＝-2x+4與y軸圍成的三角形的面積．
【答案】（1）y＝2x-2 （2）x=1 （3）
【解析】試題分析：（1）利用待定系數法將坐標代入解析式，解方程組即可得解析式，經過給的兩點即可畫出函數的圖象；
（2）觀察圖象即可得；
（3）求出兩個函數圖象的交點，兩函數圖象與y軸的交點，然后利用三角形面積公式即可得.
試題解析：（1）由一次函數y1＝kx＋b的圖像經過點（0，-2），（2，2），則有
，解得： 
，所以解析式為：y＝2x-2，
圖象如圖所示；
（2）觀察圖象可知當y=0時，x=1，
故答案為：1；
（3）由直線y2＝-2x+4與y軸將于點B，所以B（0，4），由A（0，-2），所以AB=6，
解方程組
， 得
，所以C（1.5，1）
所以S=
=
.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】已知正方形①、②在直線上，正方形③如圖放置，若正方形①、②的面積分別為81 cm2和144 cm2，則正方形③的邊長為（ ）
A. 225 cm B. 63 cm C. 50 cm D. 15 cm
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC=1，BC=
，在AC邊上截取AD=BC，連接BD．
（1）通過計算，判斷AD2與ACCD的大小關系；
（2）求∠ABD的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點C是線段AB上一點，△ACD和△BCE都是等邊三角形，連結AE，BD，設AE交CD于點F．
（1）求證：△ACE≌△DCB；
（2）求證：△ADF∽△BAD．
查看答案和解析>>
科目：初中數學 來源： 題型：
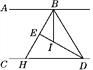
【題目】如圖，已知BE平分∠ABD，DE平分∠BDC，且∠EBD＋∠EDB＝90°.
(1)試說明：AB∥CD；
(2)H是BE的延長線與直線CD的交點，BI平分∠HBD，寫出∠EBI與∠BHD的數量關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某鄉村距城市50km,甲騎自行車從鄉村出發進城，出發1小時30分后，乙騎摩托車也從鄉村出發進城，結果比甲先到1小時，已知乙的速度是甲的2.5倍，求甲、乙兩人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】試題分析：設甲的速度是
則乙的速度是
甲、乙所用時間分別為: 
小時、
小時;根據題意可得甲比乙多用2.5小時,從而可得關于
的方程,解方程即可解答此題;注意,最后要結合題意驗根.
試題解析：設甲的速度是
則乙的速度是
根據題意列方程,得
整理,得
，
解得： 
經檢驗, 
是原方程的解.
則
答:甲的速度是12km/h,乙的速度是30km/h.
【題型】解答題
【結束】
24
【題目】已知
求
的值 。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，動點P從點C出發，按C→B→A的路徑，以2cm每秒的速度運動，設運動時間為t秒，當t為時，△ACP是等腰三角形．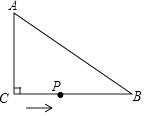 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成證明并寫出推理根據
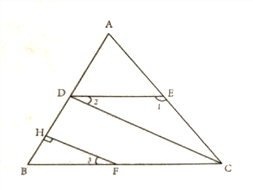
已知，如圖，∠1=132
，∠ACB=48，∠2=∠3，FH⊥AB于H，
求證：CD⊥AB．
證明:∵∠1=132, ∠ACB=48
∴∠l+∠ACB=180
∴DE∥BC
∴∠2=∠DCB（ ）
又∵∠2=∠3
∴∠3=∠DCB（ ）
∴HF∥DC （ ）
∴∠CDB=∠FHB. （ ）
又∵FH⊥AB,
∴∠FHB=90
∴∠CDB=
∴CD⊥AB. （ ）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
