
【題目】小王購買了一套經濟適用房,他準備將地面鋪上地磚,地面結構如圖所示.根據圖中的數據(單位:m),解答下列問題: 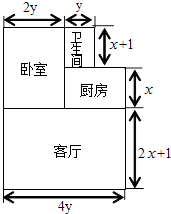
(1)寫出用含x、y的代數式表示廚房的面積是m2;臥室的面積是 m2;
(2)寫出用含x、y的代數式表示這套房的總面積是多少平方米?
(3)當x=3,y=2時,求小王這套房的總面積是多少平方米?
(4)若在(3)中,小王到某商店挑選了80cm×80cm的地磚來鑲客廳和臥室,他應買多少塊才夠用?(結果保留整數)
【答案】
(1)2xy;4xy+2y
(2)解:y(x+1)+x2y+(2x+1)2y+(2x+1)4y
=xy+y+2xy+4xy+2y+8xy+4y
=15xy+7y
(3)解:當x=3,y=2時,
原式=15×3×2+7×2
=90+14
=104(平方米),
即小王這套房的總面積是104平方米
(4)解:(2x+1)2y+(2x+1)4y
=4xy+2y+8xy+4y
=12xy+6y
當x=3,y=2時,
原式=12×3×2+6×2
=72+12
=84(平方米),
所以他應買地磚:84÷(0.8×0.8)=84÷0.64≈132(塊),
即他應買132塊才夠用
【解析】解:(1)由圖可得, 廚房的面積是:x(4y﹣2y)=2xy,
臥室的面積是:2y(x+x+1)=4xy+2y,
所以答案是:2xy;4xy+2y
【考點精析】通過靈活運用代數式求值,掌握求代數式的值,一般是先將代數式化簡,然后再將字母的取值代入;求代數式的值,有時求不出其字母的值,需要利用技巧,“整體”代入即可以解答此題.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:
【題目】已知點O是等腰直角三角形ABC斜邊上的中點,AB=BC,E是AC上一點,連結EB.
(1) 如圖1,若點E在線段AC上,過點A作AM⊥BE,垂足為M,交BO于點F.求證:OE=OF;
(2)如圖2,若點E在AC的延長線上,AM⊥BE于點M,交OB的延長線于點F,其它條件不變,則結論“OE=OF”還成立嗎?如果成立,請給出證明;如果不成立,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小學校園足球對22名隊員年齡情況如下:
年齡/歲 | 9 | 10 | 11 | 12 |
人數 | 2 | 6 | 10 | 4 |
則這個隊隊員年齡的眾數和中位數分別是( )
A.11,10
B.10,11
C.10,9
D.11,11
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“愛滿揚州”慈善一日捐活動中,學校團總支為了了解本校學生的捐款情況,隨機抽取了50名學生的捐款數進行了統計,并繪制成統計圖.

(1)這50名同學捐款的眾數為 元,中位數為 元;
(2)求這50名同學捐款的平均數;
(3)該校共有600名學生參與捐款,請估計該校學生的捐款總數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(﹣3,0),對稱軸為直線x=﹣1,下列給出四個結論中,正確結論的個數是( )個
①c>0;
②若點B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)為函數圖象上的兩點,則y1<y2;
,y2)為函數圖象上的兩點,則y1<y2;
③2a﹣b=0;
④![]() <0;
<0;
⑤4a﹣2b+c>0.
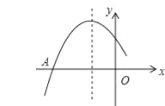
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
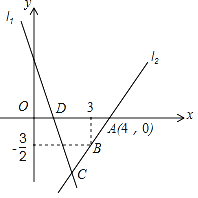
【題目】如圖,直線l1的解析表達式為y=﹣3x+3,且l1與x軸交于點D.直線l2經過點A、B,直l1,l2交于點C.
(1)求點D的坐標;
(2)求直線l2的解析表達式;
(3)在直線l2上存在異于點C的另一個點P,使得△ADP與△ADC的面積相等,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現定義新運算“※”,對任意有理數a、b,規定a※b=ab+a﹣b,
例如:1※2=1×2+1﹣2=1,(1)求3※(﹣5)的值;
(2)若(-3)※b與b,互為相反數,求b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了估計湖里有多少條魚,我們從湖里捕捉100條做標記,然后放回湖里去,經過一段時間,待帶標記的魚完全混合于魚群中,再捕第二次樣品魚200條,若其中帶標記的魚有25條,則估計湖里有魚_____________條.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com