【題目】有甲、乙兩家草莓采摘園，草莓的銷售價格相間，在生長旺季，兩家均排出優惠方案.甲園的優惠方案是:采摘的草莓不超過
時，按原價銷售；若超過
超過部分
折優惠；乙園的優惠方案是:游客進園需購買
元門票.采摘的草莓直接按降價出售.已知在甲園、乙園采摘草莓
時，所需費用相同.
在乙采摘園所需費用
( 元)與草梅采摘量
(千克)滿足一次函數關系，如下表:
數量 |
|
|
|
| ··· |
費用 |
|
|
|
| ··· |
（1）求與的函數關系式(不必寫出的范圍)；
（2）求兩個采摘園的草莓在生長旺季前的銷售價格.并求在甲采摘園所需費用
(元)與草莓采摘量(千克)的函數關系式
；
（3）若嘉琪準備花費
元去采摘草莓，去哪個園采摘，可以得到更多數量的草莓？ 說明理由.
【答案】（1）
；（2）
；（3）去乙園采摘可以得到更多數量的草莓.
【解析】
（1）根據表格數據，利用待定系數法由當
時，
； 當
時，
即可求解；
（2）設草莓在生長旺季前的銷售價格為
元/千克，根據在甲園、乙園采摘草莓
時，所需費用相同列方程即可求出銷售價格為元/千克；依據收費規則直接可得；
（3）利用已求出函數解析式分別求出當花費
元可得草莓數量進行比較即可解答．
解:（1）設
與
的函數關系式為
當時，；
當時，
解得:
．
（2）設草莓在生長旺季前的銷售價格為元/千克，根據題意，得：
解得:
(元/千克)．
．
答：去乙園采摘可以得到更多數量的草莓．
當
時，有:
．
解得
；
當
時，
，
，
解得
，
．
去乙園采摘可以得到更多數量的草莓．
科目：初中數學 來源： 題型：
【題目】已知：如圖，在平面直角坐標系，直線AB與x軸交于點A(-2，0)，與反比例函數在第一象限內的圖象的交于點B(2，n)，連接BO，若
=4．
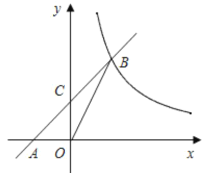
(1)求該反比例函數的解析式和直線AB的解析式；
(2)設直線AB交y軸于點C，點C是否為線段AB的中點？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面是小王同學“過直線外一點作該直線的平行線”的尺規作圖過程．
已知：直線l及直線l外一點P．
求作：直線
，使得
．
作法：如圖，
①在直線l外取一點A，作射線
與直線l交于點B，
②以A為圓心，
為半徑畫弧與直線l交于點C，連接
，
③以A為圓心，為半徑畫弧與線段交于點
，
則直線即為所求．
根據小王設計的尺規作圖過程，，
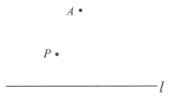
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：∵
，
∴
，（______________________）（填推理的依據）．
∵
__________，
∴
．
∵
，
∴
．
∴
（____________________）（填推理的依據）．
即．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數
的圖象經過點
（0，-4）和
（-2，2）.
（1）求
的值，并用含
的式子表示
；
（2）求證：此拋物線與
軸有兩個不同交點；
（3）當
時，若二次函數滿足
隨的增大而減小，求的取值范圍；
(4) 直線
上有一點
（
，5），將點向右平移4個單位長度，得到點
，若拋物線與線段
只有一個公共點，求的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=AC，以AB為直徑的⊙O與BC相交于點D，與CA的延長線相交于點E，過點D作DF⊥AC于點F．
（1）試說明DF是⊙O的切線；
（2）若AC=3AE，求tanC．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在邊長為
的正方形ABCD中，點E，F是對角線AC的三等分點，點P在正方形的邊上，則滿足PE+PF=
的點P的個數是（ ）
A.0B.4C.8D.16
查看答案和解析>>
科目：初中數學 來源： 題型：
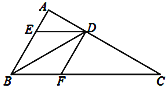
【題目】如圖，BD是△ABC的角平分線，過點D作DE∥BC交AB于點E，DF∥AB交BC于點F．
⑴求證:四邊形BEDF為菱形;
⑵如果∠A＝100°,∠C＝30°,求∠BDE的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
