
【題目】如圖,在平面直角坐標系xOy中,已知直線AC的解析式為y=﹣![]() x+1,直線AC交x軸于點C,交y軸于點A.
x+1,直線AC交x軸于點C,交y軸于點A.
(1)若等邊△OBD的頂點D與點C重合,另一頂點B在第一象限內,直接寫出點B的坐標;
(2)過點B作x軸的垂線l,在l上是否存在一點P,使得△AOP的周長最小?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)試在直線AC上求出到兩坐標軸距離相等的所有點的坐標.

【答案】(1)B(2,2![]() );(2)點P的坐標為(2,
);(2)點P的坐標為(2,![]() );(3)在直線AC上求出到兩坐標軸距離相等的點的坐標為(
);(3)在直線AC上求出到兩坐標軸距離相等的點的坐標為(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】分析:如圖,在平面直角坐標系xOy中,已知直線AC的解析式為y=﹣![]() x+1,直線AC交x軸于點C,交y軸于點A.
x+1,直線AC交x軸于點C,交y軸于點A.
(1)若等邊△OBD的頂點D與點C重合,另一頂點B在第一象限內,直接寫出點B的坐標;
(2)過點B作x軸的垂線l,在l上是否存在一點P,使得△AOP的周長最小?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)試在直線AC上求出到兩坐標軸距離相等的所有點的坐標.
詳解:(1)在y=﹣![]() x+1中,令y=0可求得x=4,
x+1中,令y=0可求得x=4,
∴D(4,0),
過B作BE⊥x軸于點E,如圖1,
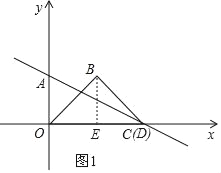
∵△OBD為等邊三角形,
∴OE=![]() OD=2,BE=
OD=2,BE=![]() OB=2
OB=2![]() ,
,
∴B(2,2![]() );
);
(2)∵等邊△OBD是軸對稱圖形,對稱軸為l,
∴點O與點C關于直線l對稱,
∴直線AC與直線l的交點即為所求的點P,
把x=2代入y=﹣![]() x+1,得y=
x+1,得y=![]() ,
,
∴點P的坐標為(2,![]() );
);
(3)設滿足條件的點為Q,其坐標為(m,﹣![]() m+1),
m+1),
由題意可得﹣![]() m+1=m或﹣
m+1=m或﹣![]() m+1=﹣m,
m+1=﹣m,
解得m=![]() 或m=﹣
或m=﹣![]() ,
,
∴在直線AC上求出到兩坐標軸距離相等的點的坐標為(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,是由相同的花盆按一定的規律組成的形如正多邊形的圖案,其中第1個圖形共有6個花盆,第2個圖形一共有12個花盆,第3個圖形一共有20個花盆,…,則第10個圖形中花盆的個數為( )

A. 110B. 120C. 132D. 140
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上的A、B兩點所表示的數分別為a、b,a+b<0,ab<0.

(1)原點O的位置在
A.點A的右邊
B.點B的左邊
C.點A與點B之間 ,且靠近點A
D.點A與點B之間 ,且靠近點B
(2)若a-b=2,
①利用數軸比較大小,a 1,b -1;(填“>”、“<”或“=”).
②化簡:|a-1|+|b+1|.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AE平分∠BAD,交BC于E,過E做EF⊥AD于F,連接BF交AE于P,連接PD.

(1)求證:四邊形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知線段a、b
(1)求作一個等腰△ABC,使底邊長BC=a,底邊上的高為b.(尺規作圖,只保留作圖痕跡)
(2)小明由此想到一個命題:等腰三角形底邊的中點到兩腰的距離相等,請你判斷這個命題的真假,如果是真命題請證明;如果是假命題請舉出反例.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一邊長為36cm的正方形硬紙板進行適當的剪裁,折成一個長方體盒子(紙板的厚度忽略不計)
(1)如圖,若在正方形硬紙板的四角各剪一個同樣大小的正方形,將剩余部分折成一個無蓋的長方體盒子.
①要使折成的長方體盒子的底面積為676cm2,那么剪掉的正方形的邊長為多少?
②折成的長方形盒子的側面積是否有最大值?如果有,求出這個最大值和此時剪掉的正方形的邊長;如果沒有,說明理由.
(2)若在正方形硬紙板的四周剪掉一些矩形(即剪掉的矩形至少有一條邊在正方形硬紙板的邊上),將剩余部分折成一個有蓋的長方體盒子,若折成的一個長方體盒子的表面積為880cm2,求此時長方體盒子的長、寬、高(只需求出符合要求的一種情況)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圓,D是優弧AmC上任意一點(不包括A,C),記四邊形ABCD的周長為y,BD的長為x,則y關于x的函數關系式是( )
,⊙O是△ABC的外接圓,D是優弧AmC上任意一點(不包括A,C),記四邊形ABCD的周長為y,BD的長為x,則y關于x的函數關系式是( )
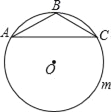
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有兩個小機器人A、B在一條筆直的道路上由西向東行走,兩機器人相距6cm,即AB=6cm.其中機器人A的速度為3cm/s,機器人B的速度為2cm/s.設機器人B行走的時間為t(s).
(1)若兩機器人同時出發,
①當t=![]() 時,AB= cm;當t=7時,AB= cm;
時,AB= cm;當t=7時,AB= cm;
②當兩機器人相距4cm時,求機器人B行走的時間t的值;
(2)若機器人B先行走2s,機器人A再行走,當兩機器人相距10cm時,請直接寫出t的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
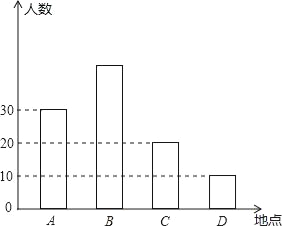
【題目】如圖,暑假快要到了,某市準備組織同學們分別到A,B,C,D四個地方進行夏令營活動,前往四個地方的人數.
(1)去B地參加夏令營活動人數占總人數的40%,根據統計圖求去B地的人數?
(2)若一對姐弟中只能有一人參加夏令營,姐弟倆提議讓父親決定.父親說:現有4張卡片上分別寫有1,2,3,4四個整數,先讓姐姐隨機地抽取一張后放回,再由弟弟隨機地抽取一張.若抽取的兩張卡片上的數字之和是5的倍數則姐姐參加,若抽取的兩張卡片上的數字之和是3的倍數則弟弟參加.用列表法或樹形圖分析這種方法對姐弟倆是否公平?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com