
【題目】在環境創優活動中,某居民小區要在一塊靠墻(墻長25米)的空地上修建一個矩形養雞場,養雞場的一邊靠墻,如果用60m長的籬笆圍成中間有一道籬笆的養雞場,設養雞場平行于墻的一邊BC的長為x(m),養雞場的面積為y(m2)
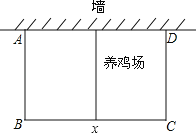
(1)求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)養雞場的面積能達到300m2嗎?若能,求出此時x的值,若不能,說明理由;
(3)根據(1)中求得的函數關系式,判斷當x取何值時,養雞場的面積最大?最大面積是多少?
【答案】(1)y=x![]() (60﹣x)=﹣
(60﹣x)=﹣![]() x2+20x(0<x≤25);(2)不能,見解析;(3)當x取25m時,養雞場的面積最大,最大面積是
x2+20x(0<x≤25);(2)不能,見解析;(3)當x取25m時,養雞場的面積最大,最大面積是![]() m2.
m2.
【解析】
試題分析:(1)先用x表示出AB,根據矩形的面積公式得到y=﹣![]() x2+20x,然后利用墻長25米可得到x的取值范圍;
x2+20x,然后利用墻長25米可得到x的取值范圍;
(2)令y=300得到﹣![]() x2+20x=300,解得x=30,然后根據x的取值范圍可判斷養雞場的面積不能達到300m2;
x2+20x=300,解得x=30,然后根據x的取值范圍可判斷養雞場的面積不能達到300m2;
(3)把(1)中的解析式配成頂點式,然后利用二次函數的性質求解.
解:(1)BC=x,則AB=![]() (60﹣x),
(60﹣x),
所以y=x![]() (60﹣x)=﹣
(60﹣x)=﹣![]() x2+20x(0<x≤25);
x2+20x(0<x≤25);
(2)不能.理由如下:
當y=300時,即﹣![]() x2+20x=300,
x2+20x=300,
整理得x2﹣60x+900=0,解得x1=x2=30,
因為0<x≤25,
所以x=30不滿足條件,
所以養雞場的面積能達到300m2;
(3)y=﹣![]() x2+20x=﹣
x2+20x=﹣![]() (x﹣30)2+300,
(x﹣30)2+300,
因為0<x≤25,
所以當x=25時,y的值最大,最大值為﹣![]() (25﹣30)2+300=
(25﹣30)2+300=![]() .
.
答:當x取25m時,養雞場的面積最大,最大面積是![]() m2.
m2.


科目:初中數學 來源: 題型:
【題目】已知兩點P(1,1)、Q(1,-1),若點Q固定,點P繞點Q旋轉使線段PQ∥x軸,則此時的點P的坐標是_________________________;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:
油桶制造廠的某車間主要負責生產制造油桶用的圓形鐵片和長方形鐵片,該車間有工人42人,每個工人平均每小時可以生產圓形鐵片120片或者長方形鐵片80片.如圖,一個油桶由兩個圓形鐵片和一個長方形鐵片相配套.生產圓形鐵片和長方形鐵片的工人各為多少人時,才能使生產的鐵片恰好配套?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在長方形ABCD中,AB=4,BC=![]() ,O為BC上一點,BO=
,O為BC上一點,BO=![]() ,如圖所示,以BC所在直線為x軸,O為坐標原點建立平面直角坐標系,M為線段OC上的一點.
,如圖所示,以BC所在直線為x軸,O為坐標原點建立平面直角坐標系,M為線段OC上的一點.
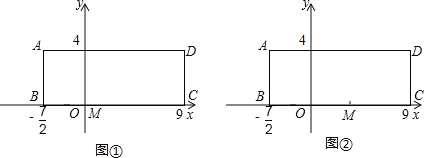
(1)若點M的坐標為(1,0),如圖①,以OM為一邊作等腰△OMP,使點P在y軸上,則符合條件的等腰三角形有幾個?請直接寫出所有符合條件的點P的坐標;
(2)若點M的坐標為(1,0),如圖①,以OM為一邊作等腰△OMP,使點P落在長方形ABCD的一邊上,則符合條件的等腰三角形有幾個?請直接寫出所有符合條件的點P的坐標.
(3)若將(2)中的點M的坐標改為(4,0),其它條件不變,如圖②,那么符合條件的等腰三角形有幾個?求出所有符合條件的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經統計我市去年共引進世界500強外資企業19家,累計引進外資410000000美元,數字410000000用科學記數法表示為( )
A.41×107 B.4.1×108 C.4.1×109 D.0.41×109
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等邊△ABC中,D是邊AC上一點,連接BD,將△BCD繞點B逆時針旋轉60°,得到△BAE,連接ED,若BC=10,BD=9.則下列結論錯誤的是( )
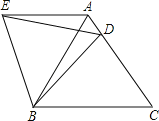
A.AE∥BC
B.△ADE的周長是19
C.△BDE是等邊三角形
D.∠ADE=∠BDC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com