
平行四邊形ABCD在平面直角坐標系中的位置如圖所示,其中A(﹣4,0),B(2,0),C(3,3)反比例函數(shù) 的圖象經(jīng)過點C.
的圖象經(jīng)過點C.
(1)求此反比例函數(shù)的解析式;
(2)將平行四邊形ABCD沿x軸翻折得到平行四邊形AD′C′B,請你通過計算說明點D′在雙曲線上;
(3)請你畫出△AD′C,并求出它的面積.
解:(1)∵點C(3,3)在反比例函數(shù) 的圖象上,∴
的圖象上,∴ 。∴m=9。
。∴m=9。
∴反比例函數(shù)的解析式為 。
。
(2)過C作CE⊥x軸于點E,過D作DF⊥x軸于點F,則△CBE≌△DAF,
∴AF=BE,DF=CE。
∵A(﹣4,0),B(2,0),C(3,3),
∴DF=CE=3,OA=4,OE=3,OB=2。
∴ 。
。
∴D(﹣3,3)。
∵點D′與點D關于x軸對稱,∴D′(﹣3,﹣3)。
把x=﹣3代入 得,y=﹣3,∴點D′在雙曲線上。
得,y=﹣3,∴點D′在雙曲線上。
(3)作圖如下:
∵C(3,3),D′(﹣3,﹣3),∴點C和點D′關于原點O中心對稱。
∴D′O=CO= D′C。
D′C。
∴S△AD′C=2S△AOC=2× AO•CE=2×
AO•CE=2× ×4×3=12。
×4×3=12。
解析試題分析:(1)把點C(3,3)代入反比例函數(shù) ,求出m,即可求出解析式。
,求出m,即可求出解析式。
(2)過C作CE⊥x軸于點E,過D作DF⊥x軸于點F,則△CBE≌△DAF,根據(jù)線段之間的數(shù)量關系進一步求出點D的坐標,再點D′與點D關于x軸對稱,求出D′坐標,進而判斷點D′是不是在雙曲線。
(3)根據(jù)C(3,3),D′(﹣3,﹣3)得到點C和點D′關于原點O中心對稱,進一步得出D′O=CO= D′C,由S△AD′C=2S△AOC=2×
D′C,由S△AD′C=2S△AOC=2× AO•CE求出面積的值。
AO•CE求出面積的值。


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:初中數(shù)學 來源: 題型:解答題
(1)先求解下列兩題:
①如圖①,點B,D在射線AM上,點C,E在射線AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度數(shù);
②如圖②,在直角坐標系中,點A在y軸正半軸上,AC∥x軸,點B,C的橫坐標都是3,且BC=2,點D在AC上,且橫坐標為1,若反比例函數(shù) (x>0)的圖象經(jīng)過點B,D,求k的值.
(x>0)的圖象經(jīng)過點B,D,求k的值.
(2)解題后,你發(fā)現(xiàn)以上兩小題有什么共同點?請簡單地寫出.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
如圖,一次函數(shù)的圖象與x軸,y軸分別相交于A,B兩點,且與反比例函數(shù) 的圖象在第二象限交與點C,如果點A為的坐標為(2,0),B是AC的中點.
的圖象在第二象限交與點C,如果點A為的坐標為(2,0),B是AC的中點.
(1)求點C的坐標;
(2)求一次函數(shù)的解析式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
已知平面直角坐標系xOy(如圖),直線 經(jīng)過第一、二、三象限,與y軸交于點B,點A(2,t)在這條直線上,連接AO,△AOB的面積等于1.
經(jīng)過第一、二、三象限,與y軸交于點B,點A(2,t)在這條直線上,連接AO,△AOB的面積等于1.
(1)求b的值;
(2)如果反比例函數(shù) (
( 是常量,
是常量, )的圖像經(jīng)過點A,求這個反比例函數(shù)的解析式.
)的圖像經(jīng)過點A,求這個反比例函數(shù)的解析式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
已知反比例函數(shù) 的圖象與一次函數(shù)
的圖象與一次函數(shù) 的圖象交于A
的圖象交于A 、B
、B 兩點,連結AO。
兩點,連結AO。
(1)求反比例函數(shù)和一次函數(shù)的表達式;
(2)設點C在y軸上,且與點A、O構成等腰三角形,請直接寫出點C的坐標。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
如圖,直線l:y=x+1與x軸、y軸分別交于A、B兩點,點C與原點O關于直線l對稱.反比例函數(shù) 的圖象經(jīng)過點C,點P在反比例函數(shù)圖象上且位于C點左側,過點P作x軸、y軸的垂線分別交直線l于M、N兩點.
的圖象經(jīng)過點C,點P在反比例函數(shù)圖象上且位于C點左側,過點P作x軸、y軸的垂線分別交直線l于M、N兩點.
(1)求反比例函數(shù)的解析式;
(2)求AN•BM的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
如圖,在平面直角坐標系xOy中,一次函數(shù)y=kx+b與反比例函數(shù) 的圖象交于點A,與x軸交于點B,AC⊥x軸于點C,
的圖象交于點A,與x軸交于點B,AC⊥x軸于點C, ,AB=
,AB=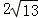 ,OB=OC.
,OB=OC.
(1)求反比例函數(shù)和一次函數(shù)的解析式;
(2)若一次函數(shù)與反比例函數(shù)的圖象的另一交點為D,作DE⊥y軸于點E,連接OD,求△DOE的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
如圖,點A(m,m+1),B(m+1,2m-3)都在反比例函數(shù) 的圖象上.
的圖象上.
(1)求m,k的值;
(2)如果M為x軸上一點,N為y軸上一點, 以點A,B,M,N為頂點的四邊形是平行四邊形,試求直線MN的函數(shù)表達式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:單選題
如圖,直線l∥m,將含有45°角的三角板ABC的直角頂點C放在直線m上,若∠1=25°,則∠2的度數(shù)為( )
| A.20° | B.25° | C.30° | D.35° |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com