
【題目】如圖,在菱形ABCD中,∠B= 60°.
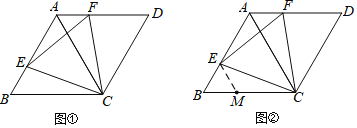
(1)如圖①.若點E、F分別在邊AB、AD上,且BE=AF,求證:△CEF是等邊三角形.
(2)小明發現,當點E、F分別在邊AB、AD上,且∠CEF=60°時,△CEF也是等邊三角形,
并通過畫圖驗證了猜想;小麗通過探索,認為應該以CE= EF為突破口,構造兩個全等三角形:小倩受到小麗的啟發,嘗試在BC上截取BM =BE,并連接ME,如圖②,很快就證明了△CEF是等邊三角形.請你根據小倩的方法,寫出完整的證明過程.
【答案】(1)見解析;(2)見解析.
【解析】
(1)易證△BEC≌△AFC,即可得證;(2)先證得△BEM是等邊三角形,再證△MEC≌AFE,即可EC=EF,再由∠CEF=60°即可證明.
(1)因為四邊形ABCD是菱形,所以AB= BC=CD=AD.
因為∠B=60°,所以△ABC,△ADC都是等邊三角形.
所以BC=AC,∠B=∠CAF=∠ACB=60°,
又因為BE=AF,所以.△BEC≌△AFC(SAS),所以CE=CF,∠ECF=∠BCA=60°
所以△ECF是等邊三角形,
(2) 因為BE=BM,∠B= 60°
所以△BEM是等邊三角形.
所以∠EMB=∠BEM=60°,∠EMC=∠AEM=120°
因為AB= BC,∠EAF120°,所以.AE=CM,∠EAF=∠EM.
因為∠FEC=60°,所以∠AEF+∠CEM=60°.
又因為∠CEM+∠ECM=60°所以∠AEF=∠ECM.
所以△MEC≌AFE(ASA),所以EC=EF.
又因為∠FEC=60°,所以△EFC是等邊三角形.


科目:初中數學 來源: 題型:
【題目】某種流感病毒,有一人患了這種流感,在每輪傳染中一人將平均傳給x人.
(1)求第一輪后患病的人數;(用含x的代數式表示)
(2)在進入第二輪傳染之前,有兩位患者被及時隔離并治愈,問第二輪傳染后總共是否會有21人患病的情況發生,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
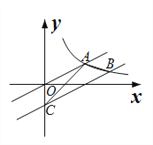
【題目】如圖,已知直線![]() 與反比例函數
與反比例函數![]() (
(![]() )圖像交于點A,將直線向右平移4個單位,交反比例函數
)圖像交于點A,將直線向右平移4個單位,交反比例函數![]() (
(![]() )圖像于點B,交y軸于點C,連結AB、AC,則△ABC的面積為_______.
)圖像于點B,交y軸于點C,連結AB、AC,則△ABC的面積為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
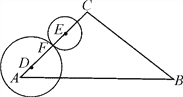
【題目】如圖,在△ABC中,∠A=45°,AB=![]() ,AC=6,點D,E為邊AC上的點,AD=1,CE=2,點F為線段DE上一點(不與D,E重合),分別以點D、E為圓心,DF、EF為半徑作圓.若兩圓與邊AB,BC共有三個交點時,線段DF長度的取值范圍是_______.
,AC=6,點D,E為邊AC上的點,AD=1,CE=2,點F為線段DE上一點(不與D,E重合),分別以點D、E為圓心,DF、EF為半徑作圓.若兩圓與邊AB,BC共有三個交點時,線段DF長度的取值范圍是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月12日華為新出的型號為“P30 Pro”的手機在上海召開發布會,某華為手機專賣網店抓住商機,購進10000臺“P30 Pro”手機進行銷售,每臺的成本是4400元,在線同時向國內、國外發售.第一個星期,國內銷售每臺售價是5400元,共獲利100萬元,國外銷售也售出相同數量該款手機,但每臺成本增加400元,獲得的利潤卻是國內的6倍.
(1)求該店銷售該款華為手機第一個星期在國外的售價是多少元?
(2)受中美貿易戰影響,第二個星期,國內銷售每臺該款手機售價在第一個星期的基礎上降低m%,銷量上漲5m%;國外銷售每臺售價在第一個星期的基礎上上漲m%,并且在第二個星期將剩下的手機全部賣完,結果第二個星期國外的銷售總額比國內的銷售總額多6993萬元,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD中,E是BC上一點,F是CD延長線上一點,![]() ,連接AE,AF,EF,G為EF中點,連接AG,DG.
,連接AE,AF,EF,G為EF中點,連接AG,DG.

(1)如圖1:若![]() ,
,![]() ,求DG;
,求DG;
(2)如圖2:延長GD至M,使![]() ,過M作MN∥FD交AF的延長線于N,連接NG,若
,過M作MN∥FD交AF的延長線于N,連接NG,若![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
幻方的歷史很悠久,傳說中最早出現在夏禹時代的“洛書”,用今天的數學符號翻譯出來,就是一個三階幻方,即將若干個數組成一個正方形數陣,任意一行、一列及對角線上的數字之和都相等.如圖1,就是一個三階幻方,由1,2,3,4,5,6,7,8,9九個數字組成的一個三行三列的矩陣(如圖),其對角線、橫行、縱向的和都為15.
(1)探究:研究發現三階幻方中間的數字與9個數的和有確定的數量關系.如果設數字連續性三階幻方中間的數字是a,則幻方中9個數字之和是 (用含a的字母代數式表示)
(2)應用:請你選取一組數據構造一個三階幻方,填入到如圖2的3×3方格中,使得每行、每列、每條對角線上的三個數之和都等于21;


(3)拓展:
數陣是由幻方演化出來的另一種數字圖.將連續的奇數1,3,5,7,9…排列成數陣(如圖3),用十字框隨機框出5個數,十字框中的五數之和能等于2020嗎?并說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“不忘初心,牢記使命.”全面建設小康社會到了攻堅克難階段. 為了解2017年全國居民收支數據國家統計局組織實施了住戶收支與生活狀況調查,按季度發布.調查采用分層、多階段、與人口規模大小成比例的概率抽樣方法,在全國31個省(區、市)的1650個縣(市、區)隨機抽選16萬個居民家庭作為調查戶.已知2017年前三季度居民人均消費可支配收入平均數是2016年前三季度居民人均消費可支配收入平均數的115%,人均消費支出為11423元,根據下列兩個統計圖回答問題:(以下計算最終結果均保留整數)

(1)求年度調查的樣本容量及2017年前三季度居民人均消費可支配收入平均數(元);
(2)求在2017年前三季度居民人均消費支出中用于醫療保健所占圓心角度數;
(3)求在2017年前三季度居民人均消費支出中用于居住的金額.
查看答案和解析>>
科目:初中數學 來源: 題型:
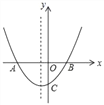
【題目】如圖,拋物線y=ax2+bx+c(a,b,c為常數,且a≠0)的圖象交x軸于A(﹣2,0)和點B,交y軸負半軸于點C,拋物線對稱軸為x=﹣![]() ,下列結論中,錯誤的結論是( )
,下列結論中,錯誤的結論是( )
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com