Question

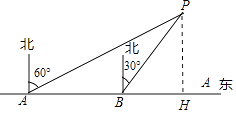
【題目】為了維護國家主權和海洋權利，海監部門對我國領海實現了常態化巡航管理，如圖，正在執行巡航任務的海監船以每小時50海里的速度向正東方航行，在A處測得燈塔P在北偏東60°方向上，繼續航行1小時到達B處，此時測得燈塔P在北偏東30°方向上．

（1）求∠APB的度數；
（2）已知在燈塔P的周圍25海里內有暗礁，問海監船繼續向正東方向航行是否安全？

Answer 1

【答案】
（1）

解：∵∠PAB=30°，∠ABP=120°，

∴∠APB=180°﹣∠PAB﹣∠ABP=30°

（2）

解：作PH⊥AB于H．

∵∠BAP=∠BPA=30°，

∴BA=BP=50，

在Rt△PBH中，PH=PBsin60°=50× =25 ，

∵25 ＞25，

∴海監船繼續向正東方向航行是安全的．

【解析】（1）在△ABP中，求出∠PAB、∠PBA的度數即可解決問題；（2）作PH⊥AB于H．求出PH的值即可判定；
【考點精析】利用三角形的內角和外角對題目進行判斷即可得到答案，需要熟知三角形的三個內角中，只可能有一個內角是直角或鈍角；直角三角形的兩個銳角互余；三角形的一個外角等于和它不相鄰的兩個內角的和；三角形的一個外角大于任何一個和它不相鄰的內角．