【題目】已知△ABC內接于⊙O，連接AO并延長交BC于點D，若∠B＝60°，∠C＝50°，則∠BAD的度數是（ ）
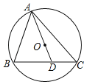
A.70°B.40°C.50°D.60°
科目：初中數學 來源： 題型：
【題目】居民區內的“廣場舞”引起媒體關注，民勤電視臺為此進行過專訪報到．小平想了解本小區居民對“廣場舞”的看法，進行了一次抽樣調查，把居民對“廣場舞”的看法分為四個層次：
．非常贊同；
．贊同但要有時間限制；
．無所謂；
．不贊同．并將調查結果繪制了圖①和圖②兩幅不完整的統計圖．請你根據圖中提供的信息解答下列問題：
（1）求本次被抽查的居民有多少人？
（2）將圖①和圖②補充完整．
（3）求圖②中“”層次所在扇形的圓心角度數．
（4）估計該小區5000名居民中對“廣場舞”的看法表示贊同（包括層次和層次）的大約有多少人．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：如果三角形的兩個內角∠α與∠β滿足∠α=2∠β，那么，我們將這樣的三角形稱為“倍角三角形”．如果一個等腰三角形是“倍角三角形”，那么這個等腰三角形的腰長與底邊長的比值為____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為弘揚傳統文化，某校開展了“傳承經典文化，閱讀經典名著”活動．為了解七、八年級學生(七、八年級各有600名學生)的閱讀效果，該校舉行了經典文化知識競賽．現從兩個年級各隨機抽取20名學生的競賽成績(百分制)進行分析，過程如下：
收集數據：
七年級：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．
八年級：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．
整理數據：
|
|
|
|
|
| |
七年級 | 0 | 1 | 0 | a | 7 | 1 |
八年級 | 1 | 0 | 0 | 7 | b | 2 |
分析數據：
平均數 | 眾數 | 中位數 | |
七年級 | 78 | 75 |
|
八年級 | 78 |
| 80.5 |
應用數據：
(1)由上表填空：a= ，b= ，c= ，d= ．
(2)估計該校七、八兩個年級學生在本次競賽中成績在90分以上的共有多少人？
(3)你認為哪個年級的學生對經典文化知識掌握的總體水平較好，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系
中（如圖），已知函數
的圖像和反比例函數的在第一象限交于A點，其中點A的橫坐標是1．
（1）求反比例函數的解析式；
（2）把直線平移后與
軸相交于點B，且
，求平移后直線的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為落實疫情期間的垃圾分類，樹立全面環保意識，某校舉行了“垃圾分類，綠色環保”知識競賽活動，根據學生的成績劃分為
，
，
，
四個等級，并繪制了不完整的兩種統計圖：
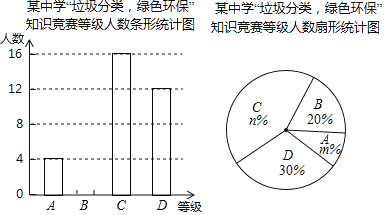
根據圖中提供的信息，回答下列問題：
（1）參加知識競賽的學生共有______人，并把條形統計圖補充完整；
（2）扇形統計圖中，
______，
______，等級對應的圓心角為______度；
（3）小明是四名獲等級的學生中的一位，學校將從獲等級的學生中任選取2人，參加市舉辦的知識競賽，請用列表法或畫樹狀圖，求小明被選中參加區知識競賽的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在美化校園的活動中，某興趣小組想借助如圖所示的直角墻角（兩邊足夠長），用28m長的籬笆圍成一個矩形花園ABCD（籬笆只圍AB，BC兩邊），設AB=xm.
（1）若花園的面積為192m2, 求x的值；
（2）若在P處有一棵樹與墻CD，AD的距離分別是15m和6m，要將這棵樹圍在花園內（含邊界，不考慮樹的粗細），求花園面積S的最大值.
查看答案和解析>>
科目：初中數學 來源： 題型：
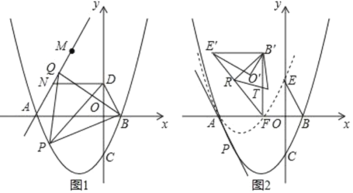
【題目】如圖，在平面直角標系中，拋物線C：y＝
與x軸交于A、B兩點（點A在點B的左側），與y軸交于點C，點D為y軸正半軸上一點．且滿足OD＝
OC，連接BD，
（1）如圖1，點P為拋物線上位于x軸下方一點，連接PB，PD，當S△PBD最大時，連接AP，以PB為邊向上作正△BPQ，連接AQ，點M與點N為直線AQ上的兩點，MN＝2且點N位于M點下方，連接DN，求DN+MN+
AM的最小值
（2）如圖2，在第（1）問的條件下，點C關于x軸的對稱點為E，將△BOE繞著點A逆時針旋轉60°得到△B′O′E′，將拋物線y＝沿著射線PA方向平移，使得平移后的拋物線C′經過點E，此時拋物線C′與x軸的右交點記為點F，連接E′F，B′F，R為線段E’F上的一點，連接B′R，將△B′E′R沿著B′R翻折后與△B′E′F重合部分記為△B′RT，在平面內找一個點S，使得以B′、R、T、S為頂點的四邊形為矩形，求點S的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
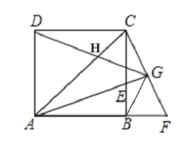
【題目】如圖，ABCD為正方形，∠CAB的角平分線交BC于點E，過點C作CF⊥AE交AE的延長線于點G，CF與AB的延長線交于點F，連接BG、DG、與AC相交于點H，則下列結論：①
ABE
CBF；②GF=CG；③BG⊥DG；④
，其中正確的是______．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
