Question

【題目】在一節數學實踐活動課上，老師拿出三個邊長都為5cm 的正方形硬紙板，他向同學們提出了這樣一個問題：若將三個正方形紙板不重疊地放在桌面上，用一個圓形硬紙板將其蓋住，這樣的圓形硬紙板的最小直徑應有多大？問題提出后，同學們經過討論，大家覺得本題實際上就是求將三個正方形硬紙板無重疊地適當放置，圓形硬紙板能蓋住時的最小直徑．老師將同學們討論過程中探索出的三種不同擺放類型的圖形畫在黑板上，如圖所示：

（1）通過計算（結果保留根號與π）．

（Ⅰ）圖①能蓋住三個正方形所需的圓形硬紙板最小直徑應為

（Ⅱ）圖②能蓋住三個正方形所需的圓形硬紙板最小直徑為

（Ⅲ）圖③能蓋住三個正方形所需的圓形硬紙板最小直徑為

(2)其實上面三種放置方法所需的圓形硬紙板的直徑都不是最小的，請你畫出用圓形硬紙板蓋住三個正方形時直徑最小的放置方法，（只要畫出示意圖，不要求說明理由），并求出此時圓形硬紙板的直徑．

Answer 1

【答案】(1) ; ; ;(2)

【解析】試題分析：（1）（Ⅰ）觀察圖形可知：圖①能蓋住三個正方形所需的圓形硬紙板最小直徑=三個正方形組成的矩形的對角線長，利用勾股定理可求出結果；（Ⅱ）圖②中圓形硬紙板的半徑是正方形的對角線長，利用勾股定理可求出結果；（Ⅲ）圖③中圓形硬紙板的直徑是正方形的對角線長的2倍，利用勾股定理可求出結果；（2）把三個正方形擺成“品”字形時，形硬紙板的直徑最小，根據勾股定理解答即可．

試題解析：（1）（Ⅰ）觀察圖形可知：圖①能蓋住三個正方形所需的圓形硬紙板最小直徑=三個正方形組成的矩形的對角線長=；（Ⅱ）圖②中圓形硬紙板的半徑=正方形的對角線長=，所以直徑=；（Ⅲ）圖③中圓形硬紙板的直徑=正方形的對角線長的2倍=；

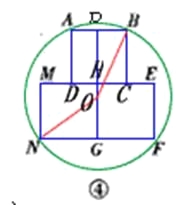
（2）如圖④為蓋住三個正方形時直徑最小的放置方法

連接OB，ON，延長OH交AB于點P，則OP⊥AB，P為AB中點設OG=x，則OP=8-x

則有：，

解得：x=

則ON=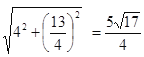，∴直徑為．