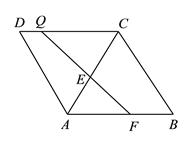
【題目】如圖，菱形
的邊
， 
， 
是
上一點， 
， 
是
邊上一動點，將梯形
沿直線
折疊， 
的對應點為
，當
的長度最小時， 
的長為__________．
科目：初中數學 來源： 題型：
【題目】列方程解應用題：
中華優秀傳統文化是中華民族的“根”和“魂”，是我們必須世代傳承的文化根脈、文化基因.為傳承優秀傳統文化，某校為各班購進《三國演義》和《水滸傳》連環畫若干套，其中每套《三國演義》連環畫的價格比每套《水滸傳》連環畫的價格貴60元，用4800元購買《水滸傳》連環畫的套數是用3600元購買《三國演義》連環畫套數的2倍，求每套《水滸傳》連環畫的價格．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（9分）某批發商以每件50元的價格購進800件T恤，第一個月以單價80元銷售，售出了200件；第二個月如果單價不變，預計仍可售出200件，批發商為增加銷售量，決定降價銷售，根據市場調查，單價每降低1元，可多售出10件，但最低單價應高于購進的價格；第二個月結束后，批發商將對剩余的T恤一次性清倉銷售，清倉是單價為40元，設第二個月單價降低
元．
（1）填表：（不需化簡）
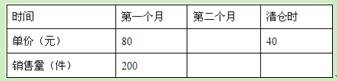
（2）如果批發商希望通過銷售這批T恤獲利9000元，那么第二個月的單價應是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，C為線段AE上一動點（不與點A，E重合），在AE同側分別作等邊△ABC和等邊△CDE，AD與BE交于點O，AD與BC交于點P，BE與CD交于點Q，連接PQ．以下五個結論：
①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP； ⑤∠AOB=60°．
其中正確的結論的個數是（ ）
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知矩形ABCD中，對角線AC、BD相交于點O，AE⊥BD，垂足為E，AD=8,
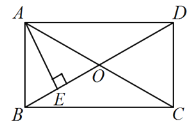
(1)若∠DAE︰∠BAE=3︰1，求∠EAC的度數；
(2)若ED=3BE，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD的對角線AC，BD相交于點O，點E，F在BD上，BE=DF．
（1）求證：AE=CF；
（2）若AB=6，∠COD=60°，求矩形ABCD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
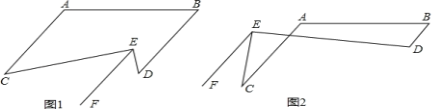
【題目】已知：∠A=（90+x）°，∠B=（90﹣x）°，∠CED=90°，射線EF∥AC，2∠C﹣∠D=m.（1）判斷AC與BD的位置關系，并說明理由．
（2）如圖1，當m=30°時，求∠C、∠D的度數．
（3）如圖2，求∠C、∠D的度數（用含m的代數式表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
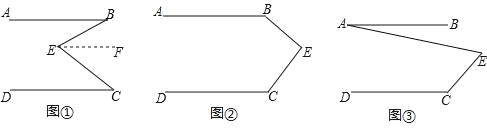
【題目】（1）問題發現：如圖①，直線AB∥CD，E是AB與CD之間的一點，連接BE，CE，可以發現∠B+∠C=∠BEC．
請把下面的證明過程補充完整：
證明：過點E作EF∥AB，
∵AB∥DC（已知），EF∥AB（輔助線的作法），
∴EF∥DC（ ）
∴∠C=∠CEF．（ ）
∵EF∥AB，∴∠B=∠BEF（同理），
∴∠B+∠C= （等式性質）
即∠B+∠C=∠BEC．
（2）拓展探究：如果點E運動到圖②所示的位置，其他條件不變，求證：∠B+∠C=360°﹣∠BEC．
（3）解決問題：如圖③，AB∥DC，試寫出∠A、∠C、∠AEC的數量關系 ．（直接寫出結論，不用寫計算過程）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，D為⊙O上一點，點C在直徑BA的延長線上，且∠CDA=∠CBD．
（1）求證：CD是⊙O的切線；
（2）過點B作⊙O的切線交CD的延長線于點E，BC=6， 
．求BE的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
