
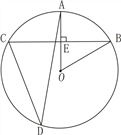
【題目】如圖,在⊙O 中,BC是弦,OA⊥BC于點E,D為⊙O上一點,連接AD,CD.
(1)求證:∠AOB=2∠ADC;
(2)若OB⊥CD,CD=8,OE=![]() ,求tan∠ADC.
,求tan∠ADC.
【答案】(1)證明見解析(2)![]()
【解析】(1)連接OC.由垂徑定理得∠AOC=∠AOB.再由圓周角定理即可得到結論;
(2)延長BO交CD于點F,連接AB.由垂徑定理得到CF的長.由∠EBO=∠FBC,∠CFB=∠OEB,得到 △ABE∽△DFC,由相似三角形對應邊成比例得到![]() .設BE=
.設BE=![]() ,則BF=4n,BC=
,則BF=4n,BC=![]() ,由勾股定理得CF=
,由勾股定理得CF=![]() ,由2n=4,得到n,BE,
,由2n=4,得到n,BE,
BO,AE的長,由tan∠ADC=tan∠ABE即可得到結論.
(1)連接OC.

∵OA⊥BC,∴弧AC=弧AB,∴∠AOC=∠AOB.
∵∠AOC=2∠ADC,∴∠AOB=2∠ADC .
(2)延長BO交CD于點F,連接AB.
∵OB⊥CD,∴CF=![]() CD=4.
CD=4.
∵∠EBO=∠FBC,∠CFB=∠OEB,
∴ △ABE∽△DFC,∴![]() .
.
設BE=![]() ,則BF=4n,BC=
,則BF=4n,BC=![]() ,
,
∴CF=![]() ,∴2n=4,n=2,∴BE=
,∴2n=4,n=2,∴BE=![]() =
=![]() ,
,
∴BO=5,AE=![]() ,∴tan∠ADC=tan∠ABE=
,∴tan∠ADC=tan∠ABE=![]() .
.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
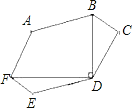
【題目】如圖所示,六邊ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,對角線FD⊥BD.已知FD=24![]() ,BD=18
,BD=18![]() .則六邊形ABCDEF的面積是______.
.則六邊形ABCDEF的面積是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,E是AD的中點,延長CE,BA交于點F,連接AC,DF.
(1)求證:四邊形ACDF是平行四邊形;
(2)當CF平分∠BCD時,寫出BC與CD的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
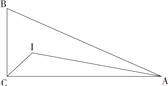
【題目】如圖,Rt△ABC中,∠ACB=90°,BC=5,AC=12,I是Rt△ABC的內心,連接CI,AI,則△CIA外接圓的半徑為()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
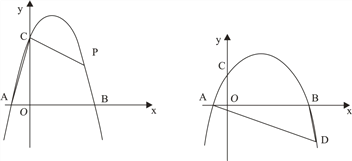
【題目】拋物線![]() 與x軸交于A,B兩點(點A在點B的左邊),與y軸正半軸交于點C.
與x軸交于A,B兩點(點A在點B的左邊),與y軸正半軸交于點C.
(1)如圖1,若A(-1,0),B(3,0),
① 求拋物線![]() 的解析式;
的解析式;
② P為拋物線上一點,連接AC,PC,若∠PCO=3∠ACO,求點P的橫坐標;
(2)如圖2,D為x軸下方拋物線上一點,連DA,DB,若∠BDA+2∠BAD=90°,求點D的縱坐標.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
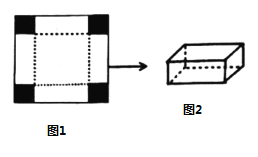
【題目】如圖1是邊長為![]() 的正方形薄鐵片,小明將其四角各剪去一個相同的小正方形(圖中陰影部分)后,發現剩余的部分能折成一個無蓋的長方體盒子,圖2為盒子的示意圖(鐵片的厚度忽略不計).
的正方形薄鐵片,小明將其四角各剪去一個相同的小正方形(圖中陰影部分)后,發現剩余的部分能折成一個無蓋的長方體盒子,圖2為盒子的示意圖(鐵片的厚度忽略不計).
(1)設剪去的小正方形的邊長為![]() ,折成的長方體盒子的容積為
,折成的長方體盒子的容積為![]() ,直接寫出用只含字母
,直接寫出用只含字母![]() 的式子表示這個盒子的高為______
的式子表示這個盒子的高為______![]() ,底面積為______
,底面積為______![]() ,盒子的容積
,盒子的容積![]() 為______
為______![]() ,
,
(2)為探究盒子的體積與剪去的小正方形的邊長![]() 之間的關系,小明列表
之間的關系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 324 |
| 588 | 576 | 500 |
| 252 | 128 |
填空:①![]() ______,
______,![]() ______;
______;
②由表格中的數據觀察可知當![]() 的值逐漸增大時,
的值逐漸增大時,![]() 的值______.(從“逐漸增大”,“逐漸減小”“先增大后減小”,“先減小后增大”中選一個進行填空)
的值______.(從“逐漸增大”,“逐漸減小”“先增大后減小”,“先減小后增大”中選一個進行填空)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com