
【題目】已知:直線AB與直線CD交于點O,過點O作OE⊥AB.
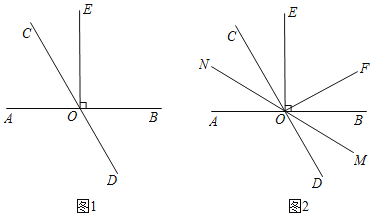
(1)如圖1,∠BOC=2∠AOC,求∠COE的度數;
(2)如圖2.在(1)的條件下,過點O作OF⊥CD,經過點O畫直線MN,滿足射線OM平分∠BOD,在不添加任何輔助線的情況下,請直接寫出與2∠EOF度數相等的角.
【答案】(1)∠COE=30°;(2)與2∠EOF度數相等的角是:∠AOD,∠BOC,∠FON,∠EOM.
【解析】
(1)先根據平角的定義可得∠AOC=60![]() ,再利用垂直的定義可得∠AOE=90
,再利用垂直的定義可得∠AOE=90![]() ,從而得結論;
,從而得結論;
(2)根據(1)中∠AOC=60![]() ,分別計算各角的度數,得其中∠EOF=60
,分別計算各角的度數,得其中∠EOF=60![]() ,根據各角的度數可得結論.
,根據各角的度數可得結論.
(1)如圖1,∵∠AOC+∠BOC=180![]() ,且∠BOC=2∠AOC,
,且∠BOC=2∠AOC,
∴∠AOC=60![]() ,
,
∵OE⊥AB,
∴∠AOE=90![]() ,
,
∴∠COE=90![]() ﹣60
﹣60![]() =30
=30![]() ;
;
(2)如圖2,由(1)知:∠AOC=60![]() ,
,
∵射線OM平分∠BOD,
∴∠BOM=∠DOM=∠AON=∠CON=30![]() ,
,
∵OE⊥AB,OC⊥OF,
∴∠AOE=∠COF=90![]() ,
,
∴∠AOC=∠EOF=60![]() ,
,
∴∠AOD=∠BOC=∠FON=∠EOM=180![]() ﹣60
﹣60![]() =120
=120![]() =2∠EOF,
=2∠EOF,
∴與2∠EOF度數相等的角是:∠AOD,∠BOC,∠FON,∠EOM.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:
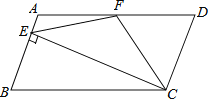
【題目】如圖,在ABCD中,AD=2AB,F是AD的中點,作CE⊥AB,垂足E在線段AB上,連接EF、CF,則下列結論中一定成立的是______.(把所有正確結論的序號都填在橫線上)①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
查看答案和解析>>
科目:初中數學 來源: 題型:
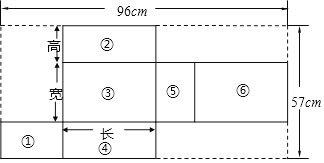
【題目】如圖是某涌泉蜜桔長方體包裝盒的展開圖.具體數據如圖所示,且長方體盒子的長是寬的2倍.
(1)展開圖的6個面分別標有如圖所示的序號,若將展開圖重新圍成一個包裝盒,則相對的面分別是 與 , 與 , 與 ;
(2)若設長方體的寬為xcm,則長方體的長為 cm,高為 cm;(用含x的式子表示)
(3)求這種長方體包裝盒的體積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,現有一張寬為12 cm的練習紙,相鄰兩條格線間的距離均為0.6 cm.調皮的小聰在紙的左上角用印章印出一個矩形卡通圖案,圖案的頂點恰好在四條格線上,已知sinα=![]() .
.
(1)求一個矩形卡通圖案的面積;
(2)若小聰在第一個圖案的右邊以同樣的方式繼續蓋印,最多能印幾個完整的圖案?
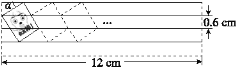
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,△ABC是等邊三角形,AE=CD,BQ⊥AD于Q,BE交AD于點P,下列說法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正確的個數有( )個。
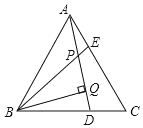
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠1=∠2,EG 平分∠AEC.
(1)如圖1,∠MAE=50°,∠FEG=15°,∠NCE=80°.試判斷 EF 與 CD 的位置關系,并說明理由.
(2)如圖2,∠MAE=135°,∠FEG=30°,當 AB∥CD 時,求∠NCE 的度數;
(3)如圖2,試寫出∠MAE、∠FEG、∠NCE 之間滿足什么關系時,AB∥CD.
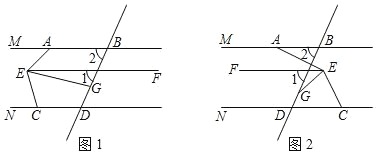
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平安路與幸福路是兩條平行的道路,且都與新興大街垂直,老街與小米胡同垂直,書店位于老街與小米胡同的交口處.如果小強同學站在平安路與新興大街交叉路口,準備去書店,按圖中的街道行走,最近的路程為( )

A. 300m B. 400m C. 500m D. 700m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com