
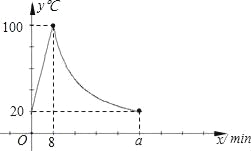
【題目】某小學為每個班級配備了一種可以加熱的飲水機,該飲水機的工作程序是:放滿水后,接通電源,則自動開始加熱,每分鐘水溫上升10℃,待加熱到100℃,飲水機自動停止加熱,水溫開始下降,水溫y(℃)和通電時間x(min)成反比例關系,直至水溫降至室溫,飲水機再次自動加熱,重復上述過程.設某天水溫和室溫為20℃,接通電源后,水溫和時間的關系如下圖所示,回答下列問題:
(1)分別求出當0≤x≤8和8<x≤a時,y和x之間的關系式;
(2)求出圖中a的值;
(3)下表是該小學的作息時間,若同學們希望在上午第一節下課8:20時能喝到不超過40℃的開水,已知第一節下課前無人接水,請直接寫出生活委員應該在什么時間或時間段接通飲水機電源.(不可以用上課時間接通飲水機電源)
時間 | 節次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一節 | |
8:30~9:05 | 第二節 | |
… | … | |
【答案】(1)當0≤x≤8時,y=10x+20; 當8<x≤a時,![]() ;(2)a=40;(3)在7:20或7:38~7:45時打開飲水機.
;(2)a=40;(3)在7:20或7:38~7:45時打開飲水機.
【解析】分析:(1)由函數圖象可設函數解析式,再由圖中坐標代入解析式,即可求得y與x的關系式;
(2)將y=20代入y=![]() ,即可得到a的值;
,即可得到a的值;
(3)要想喝到不超過40℃的熱水,讓解析式小于等于40,則可得x的取值范圍,再由題意可知開飲水機的時間.
詳解:
(1)當0≤x≤8時,設y=k1x+b,
將(0,20),(8,100)代入y=k1x+b
得k1=10,b=20
∴當0≤x≤8時,y=10x+20;
當8<x≤a時,設y=![]() ,
,
將(8,100)代入y=![]()
得k2=800
∴當8<x≤a時,y=![]() ;
;
∴當0≤x≤8時,y=10x+20;
當8<x≤a時,y=![]() ;
;
(2)將y=20代入y=![]() ,
,
解得a=40;
(3)要想喝到不超過40℃的熱水,則:
∵10x+20≤40,
∴0<x≤2,
∵![]() ≤40,
≤40,
∴20≤x<40
因為40分鐘為一個循環,
所以8:20喝到不超過40℃的開水,
則需要在8:20﹣(40+20)分鐘=7:20
或在(8:20﹣40分鐘)﹣2分鐘=7:38~7:45打開飲水機
故在7:20或7:38~7:45時打開飲水機.


 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
【題目】下列變形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 兩邊同除以
兩邊同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移項,得7x=0;
④由方程2﹣![]() 兩邊同乘以6,得12﹣x﹣5=3(x+3).
兩邊同乘以6,得12﹣x﹣5=3(x+3).
錯誤變形的個數是( )個.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義[a,b,c]為函數y=ax2+bx+c的特征數,下面給出特征數為[2m,1﹣m,﹣1﹣m]的函數的一些結論,其中不正確的是( )
A. 當m=﹣3時,函數圖象的頂點坐標是(![]() ,
,![]() )
)
B. 當m>0時,函數圖象截x軸所得的線段長度大于![]()
C. 當m≠0時,函數圖象經過同一個點
D. 當m<0時,函數在x>![]() 時,y隨x的增大而減小
時,y隨x的增大而減小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著人們生活質量的提高,凈水器已經慢慢走入了普通百姓家庭,某電器公司銷售每臺進價分別為2000元、1700元的A、B兩種型號的凈水器,下表是近兩周的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 3臺 | 5臺 | 18000元 |
第二周 | 4臺 | 10臺 | 31000元 |
(1)求A,B兩種型號的凈水器的銷售單價;
(2)若電器公司準備用不多于54000元的金額在采購這兩種型號的凈水器共30臺,求A種型號的凈水器最多能采購多少臺?
(3)在(2)的條件下,公司銷售完這30臺凈水器能否實現利潤為12800元的目標?若能,請給出相應的采購方案;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:平行四邊形ABCD的對角線AC,BD相交于點O.
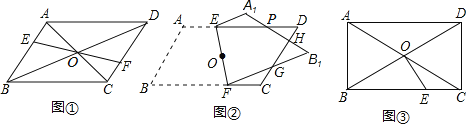
(1)如圖①,EF過點O且與AB,CD分別相交于點E、F,AC=6,△AEO的周長為10,求CF+OF的值.
(2)如圖②,將平行四邊形ABCD(紙片)沿過對角線交點O的直線EF折疊,點A落在A1處,點B落在點B1處,設FB1交CD于點G,A1B1分別交CD、DE于點H、P,請在折疊后的圖形中找一條線段,使它與EP相等,并加以證明.
(3)如圖③,△ABO是等邊三角形,AB=1,點E在BC邊上,且BE=1,則2EC-2EO= 直接填結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級兩個班,各選派10名學生參加學校舉行的“漢字聽寫”大賽.各參賽選手成績的數據分析如下表所示,則以下判斷錯誤的是( )
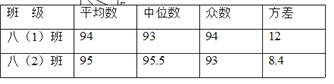
A. 八(2)班的總分高于八(1)班 B. 八(2)班的成績比八(1)班穩定
C. 八(2)班的成績集中在中上游 D. 兩個班的最高分在八(2)班
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB邊上的中點,點D、E分別在AC、BC邊上運動,且始終保持AD=CE.連接DE、DF、EF.
(1)求證:△ADF≌△CEF;
(2)試證明△DFE是等腰直角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數![]() 與
與![]() 的圖象如圖所示,則下列結論①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④ab=3k3中,正確的個數是()
的圖象如圖所示,則下列結論①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④ab=3k3中,正確的個數是()

A. 3個B. 2個C. 1個D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com