
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,頂點坐標(biāo)
,頂點坐標(biāo)![]() 且開口向下,則下列結(jié)論:①拋物線經(jīng)過點
且開口向下,則下列結(jié)論:①拋物線經(jīng)過點![]() ;②
;②![]() ;③關(guān)于
;③關(guān)于![]() 的方程
的方程![]() 有兩個不相等的實數(shù)根;④對于任意實數(shù)
有兩個不相等的實數(shù)根;④對于任意實數(shù)![]() ,
,![]() 總成立。其中結(jié)論正確的個數(shù)為( )
總成立。其中結(jié)論正確的個數(shù)為( )
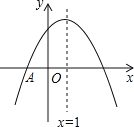
A. 1個B. 2個C. 3個D. 4個
【答案】B
【解析】
逐一分析4條結(jié)論是否正確:①根據(jù)拋物線的頂點坐標(biāo)![]() ,得出對稱軸為x=1,再根據(jù)拋物線的對稱性得出①正確;②根據(jù)拋物線的對稱軸為x=1,即可得出b+2a=0,再根據(jù)開口方向,即可得出②正確;③根據(jù)頂點坐標(biāo)
,得出對稱軸為x=1,再根據(jù)拋物線的對稱性得出①正確;②根據(jù)拋物線的對稱軸為x=1,即可得出b+2a=0,再根據(jù)開口方向,即可得出②正確;③根據(jù)頂點坐標(biāo)![]() 且開口向下,得出直線
且開口向下,得出直線![]() 與拋物線
與拋物線![]() 沒有交點,即可得出③錯誤;④拋物線開口向下,對稱軸為x=1,有最大值
沒有交點,即可得出③錯誤;④拋物線開口向下,對稱軸為x=1,有最大值![]() ,再根據(jù)x=m時的函數(shù)值為
,再根據(jù)x=m時的函數(shù)值為![]() ,由此即可得出④錯誤,綜上即可得出結(jié)論.
,由此即可得出④錯誤,綜上即可得出結(jié)論.
解:①∵拋物線y=ax2+bx+c(a≠0)的頂點坐標(biāo)![]()
∴對稱軸為x=1,
∵拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,
∴則![]() 關(guān)于對稱軸x=1的對稱點的坐標(biāo)為
關(guān)于對稱軸x=1的對稱點的坐標(biāo)為![]()
∴拋物線經(jīng)過點![]() ;∴①正確
;∴①正確
②∵拋物線的對稱軸為x=1,
∴-![]() =1,∴-2a=b,∴2a+b=0
=1,∴-2a=b,∴2a+b=0
∵開口向下,∴a![]()
∴![]() ;
;
∴②正確;
③∵![]()
∴![]()
∵頂點坐標(biāo)![]() 且開口向下,
且開口向下,
∴直線![]() 與拋物線
與拋物線![]() 沒有交點,
沒有交點,
∴關(guān)于![]() 的方程
的方程![]() 沒有實數(shù)根;
沒有實數(shù)根;
∴③錯誤;
④∵拋物線y=ax2+bx+c(a≠0)的對稱軸為x=1,開口向下
∴當(dāng)x=1,![]()
∵當(dāng)x=t時,y= at2+bt+c
∵![]() 為任意實數(shù)
為任意實數(shù)
∴![]() ≤
≤![]()
∴![]() .
.
∴![]()
∴④錯誤.
故選:B.


 課時訓(xùn)練江蘇人民出版社系列答案
課時訓(xùn)練江蘇人民出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,P為等邊三角形ABC內(nèi)的一點,且P到三個頂點A,B,C的距離分別為3,4,5,則△ABC的面積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,A,B,C三點在⊙O上,直徑BD平分∠ABC,過點D作DE∥AB交弦BC于點E,在BC的延長線上取一點F,使得EF![]() DE.
DE.
(1)求證:DF是⊙O的切線;
(2)連接AF交DE于點M,若 AD![]() 4,DE
4,DE![]() 5,求DM的長.
5,求DM的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)在把一張正方形紙片按如圖方式剪去一個半徑為40![]() 厘米的圓面后得到如圖紙片,且該紙片所能剪出的最大圓形紙片剛好能與前面所剪的扇形紙片圍成一圓錐表面,則該正方形紙片的邊長約為( )厘米.(不計損耗、重疊,結(jié)果精確到1厘米,
厘米的圓面后得到如圖紙片,且該紙片所能剪出的最大圓形紙片剛好能與前面所剪的扇形紙片圍成一圓錐表面,則該正方形紙片的邊長約為( )厘米.(不計損耗、重疊,結(jié)果精確到1厘米,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

A. 64 B. 67 C. 70 D. 73
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩種商品原來的單價和為100元.因市場變化,甲商品降價10%,乙商品提價40%,調(diào)價后兩種商品的單價和比原來的單價和提高了20%.甲、乙兩種商品原來的單價各是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】解放橋是天津市的標(biāo)志性建筑之一,是一座全鋼結(jié)構(gòu)的部分可開啟的橋梁,
(I)如圖①,已知解放橋可開啟部分的橋面的跨度AB等于47m,從AB的中點C處開啟,則AC開啟至A'C'的位置時,A'C'的長為 .
(II)如圖②,某校數(shù)學(xué)興趣小組要測量解放橋的全長PQ,在觀景平臺M處測得∠PMQ=54°,沿河岸MQ前行,在觀景平臺N處測得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放橋的全長PQ(tan54°≈1.4,tan73°≈3.3,結(jié)果保留整數(shù))

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
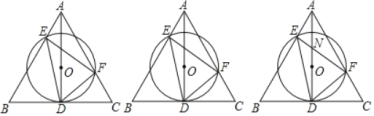
【題目】如圖:AD是正△ABC的高,O是AD上一點,⊙O經(jīng)過點D,分別交AB、AC于E、F
(1)求∠EDF的度數(shù);
(2)若AD=6![]() ,求△AEF的周長;
,求△AEF的周長;
(3)設(shè)EF、AD相較于N,若AE=3,EF=7,求DN的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
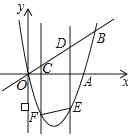
【題目】如圖,二次函數(shù)y=x2﹣4x的圖象與x軸、直線y=x的一個交點分別為點A、B,CD是線段OB上的一動線段,且CD=2,過點C、D的兩直線都平行于y軸,與拋物線相交于點F、E,連接EF.
(1)點A的坐標(biāo)為 ,線段OB的長= ;
(2)設(shè)點C的橫坐標(biāo)為m.
①當(dāng)四邊形CDEF是平行四邊形時,求m的值;
②連接AC、AD,求m為何值時,△ACD的周長最小,并求出這個最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com